1. KMP算法的基本思想
KMP算法的核心思想是当在文本中匹配模式字符串失败时,可以利用模式自身的特征,跳过一些不必要的匹配过程。具体来说,KMP算法通过构建一个部分匹配表(也称为前缀函数表或者next数组),来记录模式字符串的前缀和后缀的相同部分,从而决定下一步匹配的位置。
2. KMP算法的工作流程
KMP算法分为两个主要步骤:
- 构建next数组:next数组存储了每个位置之前的最长相同前后缀长度,用于确定在模式匹配失败时,模式应向右移动的位数。
- 在文本中进行匹配:利用next数组,在模式匹配失败时,根据next值跳转到适当的位置继续匹配,而不是回溯到最初的位置。
3. 构建next数组
1)最长公共前后缀
a. 前缀
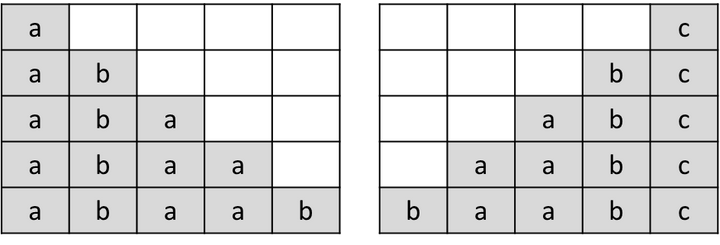
前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串。比如,对于字符串“abaabc”,它有“a”,”ab”,”aba”,”abaa”,”abaab”一共五个前缀。
b. 后缀
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。比如,对于字符串“abaabc”,它有“c”,”bc”,”abc”,”aabc”,”baabc”一共五个后缀。
c. 最长公共前后缀
按照前后缀的长度,依次进行比较,从各组相等的前后缀中,返回长度最大的一组前后缀的。比如:

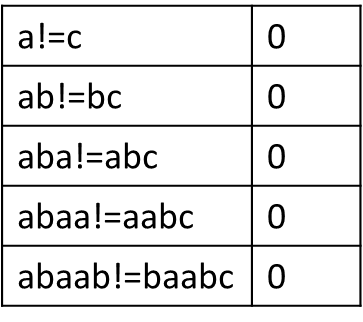
“abaabc”的前后缀

“abaabc”的最长公共前后缀长度""
所以字符串“abaabc”的最长公共前后缀长度为0
还比如,

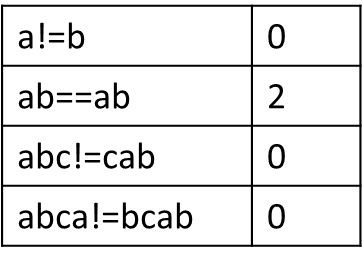
“abcab”的前后缀

abcab
所以字符串“abcab”的最长公共前后缀长度为2
注意:
- 前后缀并不是完整的字符串,而是不包括字符串首字符或者末字符的子串
- 对于单个字符,比如‘a’,它的最长公共前后缀的长度为0,因为前后缀不能是完整的字符串,必须不包括首字符或者末字符
2)next数组
next数组其实就是前缀表,比如next[j]其实表示的是当模式串第j个字符与主串匹配不成功时,需要将指针j移动至哪个位置,从该位置开始与主串重新匹配,也就是求起点为0,长度为j-1的子串的最长公共前后缀的长度。比如,当”abaaba“的第六个字符’a‘与主串匹配不成功时,需要求”abaab“的最长公共前后缀的长度,也就是’ab‘的长度2,所以j指针会移动至模式串p[2]也就是a开始重新与主串匹配。
子串的最长公共前后串长度next[j]=子串p[0,…,j−2]的最长公共前后串长度0≤j≤n
3) next数组求解
a. 暴力求解(复杂度为O(n^2))
如果主串和模式串分别为:

那么对于模式串“abaabc”
- 当第六个元素匹配失败时,那么就查看’abaab’的最长公共前后缀长度,令主串指针i不变,模式串指针j=2,因为next[5]表示“abaab”的最长公共前后缀长度,可知’ab’长度为2,所以下一次匹配时,直接从模式串的第三个字符‘a’处开始匹配,所以next[5]=2
- 当第五个元素匹配失败时,令主串指针i不变,模式串指针j=1,next[4]=1
- 当第四个元素匹配失败时,令主串指针i不变,模式串指针j=1,next[3]=1
- 当第三个元素匹配失败时,令主串指针i不变,模式串指针j=1,next[2]=0
- 当第二个元素匹配失败时,令主串指针i不变,模式串指针j=1,next[1]=0
- 当第一个元素匹配失败时,令主串指针i不变,模式串指针j=0,next[0]=-1,此时匹配下一个相邻子串,令j=-1,i++,j++
- 那么next[6]表示的就是字符串”abaabc“的最长公共前后缀长度,为0
综上,next数组表示为,且next[0]为-1,next[1]始终为0

下面即O(n^2)求next数组的代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
void get_next(vector<int>& next, string p)
{
int n = p.size();
next.assign(n + 1, 0);
for (int j = 2; j <= n; j++) {
string tmp = p.substr(0, j);
for (int len = j - 1; len >= 1; len--) {
if (tmp.substr(0, len) == tmp.substr(j - len, len))
next[j] = len;
break;
}
}
next[0] = -1;
}
|
b. O(n)求法
参考:
. - 力扣(LeetCode)
代码如下:
1
2
3
4
5
6
7
8
9
10
11
| void get_next(vector<int>& next, string p)
{
int n = p.size();
next.assign(n + 1, 0);
next[0] = -1;
for (int j = 2, i = 0; j <= n; j++) {
while (i > 0 && p[i] != p[j - 1]) i = next[i];
if (p[i] == p[j - 1]) i++;
next[j] = i;
}
}
|
c. next数组的进一步优化
拿上面的例子说明,对于模式串“abaabc”,有以下next数组

当j=2,也就是模式串指针指向第三个字符‘a’时,匹配失败,由next[2]可知,j=0,指针指向模式串第一个字符’a’,但我们可知,模式串指针是指向字符‘a’时与主串匹配失败,那么第一个字符’a’必不可能与主串当前的字符匹配,那么next[2]=0就没有意义了,因为它必定会匹配失败。
在这个基础上,我们可以直接将next[2]=-1,然后使j++,i++;如果j指向-1,那么就跳过主串的当前字符匹配下一个字符。
同理,next[4] = 1时,也就是第五个字符‘b’匹配失败时,模式串指针j会重新指向1,也就是模式串的第二个字符‘b’,但字符’b’注定会失败,而next[1]=0, 指针会重新指向第一个字符, 所以我们直接将next[4]=0.
综上,如果next数组指向的新字符与匹配失败的字符相同,那么就修改该next数组值,使其等于之前指向新位置的next值,即
next[j]=next[next[j]]
我们将新的数组称为nextval,上面的例子中,nextval等于

nextval求解代码为:
1
2
3
4
5
6
| void get_nextval(vector<int>& next, string T) {
for (int j = 1; j <= T.length(); j++) {
if (T[next[j]] == T[j])
next[j] = next[next[j]];
}
}
|
4. 模式串和主串匹配过程
针对主串s和模式串p,如果 p[j] 和 s[i]匹配失败,那么下一次就用 p[next[j]] 去和 s[i]匹配,如果仍然失败就用 p[next[next[j]]] 去和 s[i]匹配 ,直到跳转到 p[0]
1
2
3
4
5
6
7
8
9
10
11
12
13
| vector<int> kmp(string s, string p, vector<int>& next)
{
vector<int> res;
for (int i = 0, j = 0; i < s.size(); i++) {
while (j > 0 && s[i] != p[j]) j = next[j];
if (s[i] == p[j]) j++;
if (j == p.size()) {
res.push_back(i - j + 1);
j = next[j];
}
}
return res;
}
|
可通过力扣的一道题目练习kmp算法
- 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)](https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/solutions/2600821/kan-bu-dong-ni-da-wo-kmp-suan-fa-chao-qi-z1y0/)
解题代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
| #include <iostream>
#include <string>
#include <vector>
using std::string;
using std::vector;
class Solution {
public:
vector<int> GetNext(string p) {
std::size_t len = p.length();
vector<int> next(len + 1, 0);
for (int j = 1, i = 0; j < len; j++) {
while (i > 0 and p[i] != p[j]) i = next[i];
if (p[i] == p[j]) i++;
next[j + 1] = i;
}
next[0] = -1;
return next;
}
void GetNextVal(vector<int>& next, string p) {
for (int j = 1; j < p.length(); j++) {
if (p[next[j]] == p[j])
next[j] = next[next[j]];
}
}
int strStr(string haystack, string needle) {
if (needle.size() > haystack.size()) return -1;
vector<int> next = GetNext(needle);
vector<int> res;
GetNextVal(next, needle);
bool remake = false;
for (int i = 0, j = 0; i < haystack.size(); i++) {
while (j > 0 and haystack[i] != needle[j]) {
j = next[j];
if (j == -1) {
j++;
remake = true;
break;
}
}
if (remake) {
remake = false;
continue;
}
if (haystack[i] == needle[j]) j++;
if (j == needle.size()) {
res.push_back(i - j + 1);
j = next[j];
}
}
return res.size() > 0 ? res[0] : -1;
}
};
|
参考:
代码随想录programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE编辑
. - 力扣(LeetCode)leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/solutions/2600821/kan-bu-dong-ni-da-wo-kmp-suan-fa-chao-qi-z1y0/编辑