C++常见容器

2025-04-30 12:24:32 # 面试 #C++容器

1. String类

C++中有两种主要的字符串类型：

C 风格字符串（C-strings）：基于字符数组，以空字符 ('\0') 结尾。
C++ std::string 类：更高级、功能更丰富的字符串类，封装了字符串操作的复杂性。

1.1 初始化

std::string 并不像 char 是C++的基本类型，它是C++标准库的一个类，位于<string> 头文件中，它的构造函数有很多种，可通过如下方式进行初始化：

举例：

string(); // 默认构造
string (const string& str); // 拷贝构造
string (const string& str, size_t pos, size_t len = npos); // 部分拷贝
string (const char* s); 
string (const char* s, size_t n);
string (size_t n, char c);
template <class InputIterator>  string  (InputIterator first, InputIterator last);
string (initializer_list<char> il);
string (string&& str) noexcept;

std::string s0 ("Initial string");
// constructors used in the same order as described above:
std::string s1; // ""
std::string s2 (s0); // Initial string
std::string s3 (s0, 8, 3); // str
std::string s4 ("A character sequence"); // A character sequence
std::string s5 ("Another character sequence", 12); // Another char
std::string s6a (10, 'x'); // xxxxxxxxxx
std::string s6b (10, 42);      // **********
std::string s7 (s0.begin(), s0.begin()+7); // Initial

我们也可以通过赋值运算符进行 std::string 对象的初始化：

string& operator= (const string& str); // 1
string& operator= (const char* s); // 2
string& operator= (char c); // 3

std::string str1("Hello");
std::string str2 = str1; // 1
std::string str3 = "Hello"; // 2
std::string str4 == 'c'; // 3

也可以从终端读取字符进行初始化：

std::string input,line;
std::cout << "请输入一个字符串：";
std::cin >> input; // 读取直到第一个空白字符结束

std::cout << "请输入一行文本：";
std::getline(std::cin, line); // 读取包含空格的整行字符串，回车结束

1.2 字符串操作

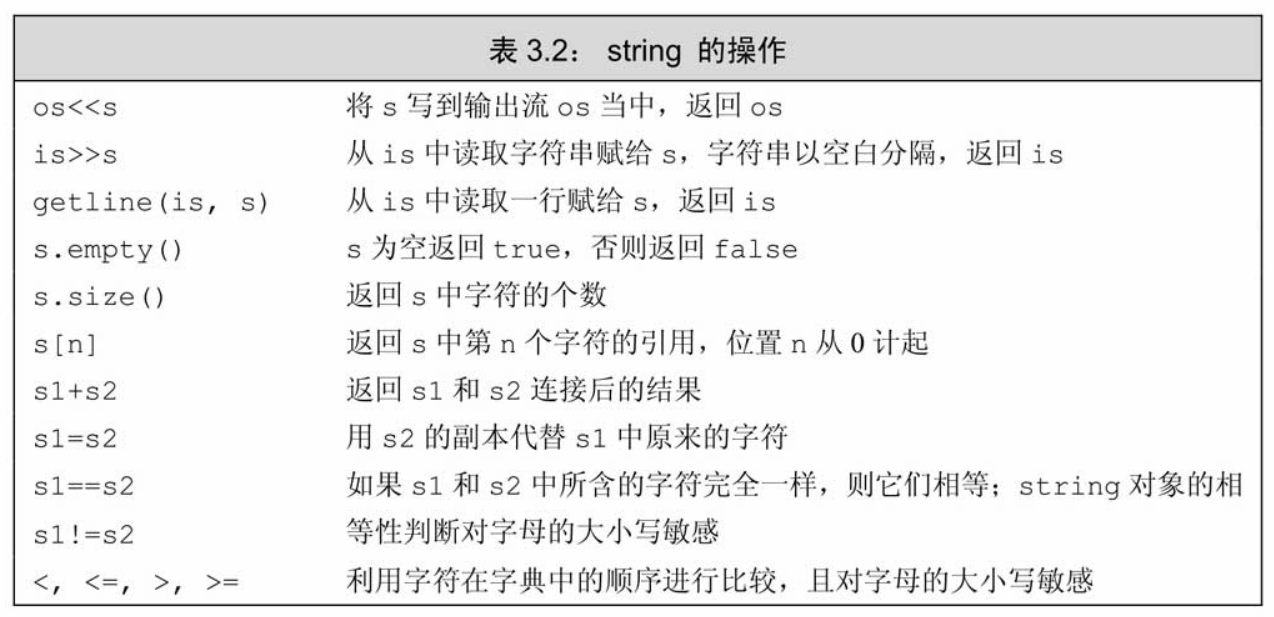
std::string 重载了很多符号，比如 =、+、!=、<、[]......，这使得它可以和其他 std::string 对象操作和比较。如下图所示：

1740814884893

1.2.1 拼接

我们可以通过 + 运算符、append() 函数以及 += 运算符将字符串拼接到指定字符串尾部，但如果想要将字符串拼接到指定字符串首部时，比如调用 + 运算符的友元函数；如果想要将字符串添加到 std::string 对象指定位置，可以使用 insert 函数：

// append添加到尾部
std::string str;
std::string str4="Writing ";
std::string str5="print 10 and then 5 more";
str.append(str4);                       // "Writing "
str.append(str5,6,3);                   // "Writing 10 "
str.append("dots are cool",5);          // "Writing 10 dots "
str.append("here: ");                   // "Writing 10 dots here: "
str.append(10,'.');                    // "Writing 10 dots here: .........."
str.append(str5.begin()+8,str5.end());  // "Writing 10 dots here: .......... and then 5 more"
str.append<int>(5,0x2E);                // "Writing 10 dots here: .......... and then 5 more....."
// + 添加到尾部
std::string name ("John");
std::string family ("Smith");
name += " K. ";         // John K. 
name += family;         // John K. Smith
name += '\n';           // John K. Smith\n
// + 友元函数添加到首部
std::string firstlevel ("com");
std::string secondlevel ("cplusplus");
std::string scheme ("http://");
std::string hostname;
std::string url;
hostname = "www." + secondlevel + '.' + firstlevel; // www.cplusplus.com
url = scheme + hostname; // http://www.cplusplus.com
// insert 到指定位置
std::string str_insert="to be question";
std::string str6="the ";
std::string str7="or not to be";
std::string::iterator it;
str_insert.insert(6,str6);                 // to be (the )question
str_insert.insert(6,str7,3,4);             // to be (not )the question
str_insert.insert(10,"that is cool",8);    // to be not (that is )the question
str_insert.insert(10,"to be ");            // to be not (to be )that is the question
str_insert.insert(15,1,':');               // to be not to be(:) that is the question
it = str_insert.insert(str_insert.begin()+5,','); // to be(,) not to be: that is the question
str_insert.insert (str_insert.end(),3,'.');       // to be, not to be: that is the question(...)
str_insert.insert (it+2,str7.begin(),str7.begin()+3); // (or )

1.2.2 清空、删除

如果我们想清空字符串，通过调用 clear() 函数可将字符串内容设置为 null：

1 2	td::string strClear("strClear"); strClear.clear(); // ""，空字符串

若想从字符串尾部删除字符，可通过 pop_back() 函数删除字符串末尾的 1 个字符：

1 2	std::string str_hello ("hello world!"); str_hello.pop_back(); // hello world

若想删除指定字符串、指定位置的子字符串，可通过 erase() 函数实习：

std::string str_erase ("This is an example sentence.");
str_erase.erase (10,8);			// "This is an sentence."	
str_erase.erase (str_erase.begin()+9); 	// "This is a sentence."
str_erase.erase (str_erase.begin()+5, str_erase.end()-9); 	// "This sentence."

1.2.3 比较字符串

关于字符串的比较，其实是逐个位置按照字符比较，计算机中字符存储的方式是ASCII码表，每个字符对应一个ASCII码值，比较字符就是比较ASCII码值的大小：

1740815787563 1740815817891

我们通过重载的 ==, !=, <, >, <=, >= 运算符可实现字符串的比较：

std::string a = "apple";
std::string b = "banana";

if (a == b) {
    std::cout << "a 和 b 相等" << std::endl;
} else {
    std::cout << "a 和 b 不相等" << std::endl;
}

if (a < b) {
    std::cout << "a 在字典序中小于 b" << std::endl;
} else {
    std::cout << "a 在字典序中不小于 b" << std::endl;
}

// a 和 b 不相等
// a 在字典序中小于 b

1.2.4 修改字符串

修改字符串大小：

我们可以通过 resize() 函数手动设置字符串的大小，比如：

将字符串的大小设置为size字符。如果size大于当前大小，则扩展字符串以使其长度为字符长，并将额外的字符添加到末尾（新字符若不指定，则默认为'\0‘）。如果size小于当前大小，则从末尾删除字符。

// resize
std::string strResize("strResize");
strResize.resize(6); // "strRes"
strResize.resize(16, '*'); // "strRes**********"

替换字符串：

我们也可以使用 replace() 函数将从索引位置开始的n个字符替换为后面的字符串，并返回对该字符串的引用：

// 替换掉字符串的字符
std::string strReplace("strReplace");
std::cout << strReplace.replace(0, 3, "STR") << '\n';	// "STRReplace"
std::cout << strReplace.replace(0, 3, 2, '*') << '\n';	// "**Replace"，从索引0开始，替换长度为3的子串为2个'*'
std::cout << strReplace.replace(strReplace.begin()+2, strReplace.begin()+5, "rep") << '\n';	// "**replace"
std::string str = "Hello, World!";
std::string replacement = "C++ Programming";
// 从索引 7 开始，替换长度为 5 的子串为 replacement 从索引 0 开始长度为 3 的子串
str.replace(7, 5, replacement, 0, 3);

交换字符串：

我们也可以使用 swap() 函数交换两个字符串：

// 交换字符串
std::string strSwap("strSwap");
std::string strSwapWhat("strSwapWhat");
strSwap.swap(strSwapWhat);
std::cout << strSwap << '\n';	// "strSwapWhat"

转换字符串格式：

我们可以转换字符串的格式，比如使用 std::stoi 将 std::string 类型转换为 int；也可以使用 std::to_string 将其他类型转换为 std::string：

std::string str = "123";
int num = std::stoi(str);
std::string str = "3.14";
double num = std::stod(str);
int num = 789;
std::string str = std::to_string(num);

1.2.5 字符串查询

查询字符串是否为空：empty()

1 2	std::string str; std::cout << str.empty() << std::endl; // 1

查询字符串的字符个数：size()、length()、capacity()、max_size()

// 返回此字符串中的字符数。相当于size()。
size_t size() const noexcept;
size_t length() const noexcept;
// 返回当前为字符串分配的存储空间的大小，字符的数量表示。
size_t capacity() const noexcept;
// 返回字符串可以达到的最大长度。
size_t max_size() const noexcept;

std::string strQuerySize("strQuerySize");
std::cout << strQuerySize.length() << '\n';	// 12
std::cout << strQuerySize.size() << '\n';	// 12
std::cout << strQuerySize.capacity() << '\n'; // 12
std::cout << strQuerySize.max_size() << '\n'; // 4611686018427387897

返回给定位置字符串的字符（不是删除）：at()、[]、back()、front()、data()、c_str()

// 获取字符串中给定位置的字符，position的范围：0 <= position < size()
char& at (size_t pos);
const char& at (size_t pos) const;

// [] 运算符，返回指定位置的字符
char& operator[] (size_t pos);
const char& operator[] (size_t pos) const;

// 返回字符串的最后一个字符，等同于at(size()-1)
char& back();
const char& back() const;

// 返回字符串的第一个字符，等同于at(0)
char& front();
const char& front() const;

// 返回指向字符串内部字符数组的指针
const char* data() const noexcept; // 不以'\0'结尾的字符数组
const char* c_str() const noexcept; // 以 '\0' 结尾的字符数组

举例：

std::string strQueryChar("strQueryChar");
std::cout << strQueryChar.at(1) << '\n';     // t
std::cout << strQueryChar[2] << '\n';        // r
std::cout << strQueryChar.back() << '\n';    // r
std::cout << strQueryChar.front() << '\n';   // s
const char* pCharArr = strQueryChar.data(); 
const char* cstrPtr = strQueryChar.c_str();

查询是否包含指定的子字符串、字符：

find：查询是否包含第一个参数指定的字符串或字符，成功则返回首次查询到的子串的索引，失败返回std::string::npos；
rfind：从末端开始查询是否包含第一个参数指定的字符串或字符，并返回首次查询到的子串的索引，失败返回std::string::npos；
find_first_of：在字符串中搜索与参数中指定的任何字符匹配的第一个字符。成功返回索引，失败返回std::string::npos；
find_last_of：在字符串中搜索与参数中指定的任何字符匹配的最后一个字符。成功返回索引，失败返回std::string::npos；

std::string str = "Hello, World! This is a test string.";
// find 函数示例
std::size_t found1 = str.find("World"); // 7
std::size_t found2 = str.find('!'); // 12
// rfind 函数示例
std::size_t rfound1 = str.rfind("is"); // 19
std::size_t rfound2 = str.rfind('t'); // 30
// find_first_of 函数示例
std::size_t found_first = str.find_first_of("aeiou"); // 1(a)
// find_last_of 函数示例
std::size_t found_last = str.find_last_of("aeiou"); // 32（i）

获取一个子字符串:

substr返回一个新构造的字符串对象，其值初始化为此对象的子字符串的副本:

1
2
3

std::string str = "Hello, World!";
std::string sub = str.substr(7, 5); // 从位置7开始，长度5
std::cout << sub << std::endl; // 输出: World

注意： 如果省略第二个参数，substr() 会返回从起始位置到字符串末尾的所有字符。

1 2	std::string sub = str.substr(7); // 从位置7开始直到结束 std::cout << sub << std::endl; // 输出: World!

1.2.6 判断字符串中的字符字母/数字/大小写

std::string 类中不包含对字符大小写/字母/数字判断的函数，需要我们包含头文件<cctype>：

1740818829188

如果我们需要将指定字符串转换为大小写，我们需要使用<algorithm> 头文件中的std::transform，并结合 <cctype> 中的std::toupper 和 std::tolower实现：

#include <iostream>
#include <string>
#include <algorithm>
#include <cctype>

int main() {
    std::string str = "Hello, World!";
    std::transform(str.begin(), str.end(), str.begin(), 
                   [](unsigned char c) { return std::toupper(c); }); // 输出: HELLO, WORLD!
    std::transform(str.begin(), str.end(), str.begin(), 
               [](unsigned char c) { return std::tolower(c); }); // 输出: hello, world!
    return 0;
}

1.3 其他高级用法

1.3.1 字符串流（`stringstream`）

std::stringstream 是 C++ 标准库中第 <sstream> 头文件提供的一个类，用于在内存中进行字符串的读写操作，类似于文件流。

#include <iostream>
#include <sstream>
#include <string>

// 从字符串流中读取数据
std::string data = "123 45.67 Hello";
std::stringstream ss(data);
int a;
double b;
std::string c;
ss >> a >> b >> c;
std::cout << "a: " << a << ", b: " << b << ", c: " << c << std::endl; // 输出: a: 123, b: 45.67, c: Hello

// 向字符串流写入数据
std::stringstream ss;
ss << "Value: " << 42 << ", " << 3.14;
std::string result = ss.str();
std::cout << result << std::endl; // 输出: Value: 42, 3.14

// 字符串拼接
std::string str1 = "Hello";
std::string str2 = ", ";
std::string str3 = "World!";
std::stringstream ss;
ss << str1 << str2 << str3;
std::string result = ss.str();
std::cout << "拼接后的字符串: " << result << std::endl; // Hello, World!

// 字符串分割
std::string str = "apple,banana,orange";
std::stringstream ss(str);
std::string token;
std::vector<std::string> tokens;
//使用 std::getline 函数从 ss 中按逗号 , 分割字符串，将分割后的每个子字符串存储在 token 中，并添加到 tokens 向量中
while (std::getline(ss, token, ',')) { //
    tokens.push_back(token);
}

1.3.2 正则表达式与字符串匹配

C++ 标准库提供了 <regex> 头文件，用于支持正则表达式。

std::string text = "The quick brown fox jumps over the lazy dog.";
std::regex pattern(R"(\b\w{5}\b)"); // 匹配所有5个字母的单词

std::sregex_iterator it(text.begin(), text.end(), pattern);
std::sregex_iterator end;

std::cout << "5个字母的单词有:" << std::endl;
while (it != end) {
    std::cout << (*it).str() << std::endl;
    ++it;
}

1.4 简单的例子

示例项目1：简易文本分析器

需求分析：

创建一个程序，接受用户输入的一段文本，并提供以下功能：

统计单词数量
统计每个单词出现的次数
查找指定单词的出现次数
输出最长的单词

#include <iostream>
#include <string>
#include <sstream>
#include <map>
#include <algorithm>

int main() {
    std::string text;
    std::cout << "请输入一段文本（结束请输入Ctrl+Z/exit()）：\n";
    
    // 读取整段文本
    std::ostringstream oss;
    std::string line;
    while (std::getline(std::cin, line)) {
        if(line == "exit()")
            break;
        oss << line << " ";
    }
    text = oss.str();

    // 使用字符串流分割单词
    std::stringstream ss(text);
    std::string word;
    std::map<std::string, int> wordCount;
    size_t totalWords = 0;
    std::string longestWord;

    while (ss >> word) {
        // 去除标点符号（简单处理）
        word.erase(std::remove_if(word.begin(), word.end(), 
            [](char c) { return ispunct(c); }), word.end());

        // 转为小写
        std::transform(word.begin(), word.end(), word.begin(), [](auto c){
            return std::tolower(c);
        });

        if (!word.empty()) {
            wordCount[word]++;
            totalWords++;
            if (word.length() > longestWord.length()) {
                longestWord = word;
            }
        }
    }

    std::cout << "\n统计结果:\n";
    std::cout << "总单词数: " << totalWords << std::endl;
    std::cout << "每个单词出现的次数:\n";
    for (const auto& pair : wordCount) {
        std::cout << pair.first << ": " << pair.second << std::endl;
    }

    std::cout << "最长的单词: " << longestWord << std::endl;

    // 查找指定单词的出现次数
    std::string searchWord;
    std::cout << "\n请输入要查找的单词: ";
    std::cin >> searchWord;
    // 转为小写
    std::transform(searchWord.begin(), searchWord.end(), searchWord.begin(), ::tolower);
    auto it = wordCount.find(searchWord);
    if (it != wordCount.end()) {
        std::cout << "'" << searchWord << "' 出现了 " << it->second << " 次。" << std::endl;
    } else {
        std::cout << "'" << searchWord << "' 未在文本中找到。" << std::endl;
    }

    return 0;
}

示例项目2：用户输入验证工具

需求分析：

编写一个程序，接受用户输入的电子邮件地址，并验证其格式是否正确。简单的验证标准：

包含一个 @ 符号
@ 后面有一个 . 符号
不包含空格

代码实现：

#include <iostream>
#include <string>
#include <regex>

bool isValidEmail(const std::string& email) {
    // 简单的正则表达式，匹配基本的邮件格式
    const std::regex pattern(R"((\w+)(\.?\w+)*@(\w+)(\.\w+)+)");
    return std::regex_match(email, pattern);
}

int main() {
    std::string email;
    std::cout << "请输入您的电子邮件地址: ";
    std::cin >> email;

    if (isValidEmail(email)) {
        std::cout << "电子邮件地址有效。" << std::endl;
    } else {
        std::cout << "电子邮件地址无效。" << std::endl;
    }

    return 0;
}

2. Vector

向量（Vector）是 C++ STL 中的一种序列式容器，能够动态地管理可变大小的连续数组。与传统的固定大小的数组不同，向量可以根据需要动态调整其大小，简单来说向量是一个能够存放任意类型的动态数组。是连续的。

注意：使用 std::vector 需要包含 <vector> 头文件

2.1 初始化

std::vector<int> vec1; // 空向量
vector<int> v{1,2,3,4,5}; //直接使用初始化列表赋值
vector<int> v(5); //初始化5个值为0的元素
vector<int> v(5, 4); //初始化5个值为4的元素
std::vector<int> v2(v1); // v1
std::vector<int> v2(std::move(vec4));

2.2 vector容器操作

2.2.1 vector的大小和容量

size()：返回 std::vector 中当前实际存储的元素数量。
capacity()：返回 std::vector 目前已经分配的内存空间能够容纳的元素数量。
empty()：检查向量是否为空。

std::vector<int> vec = {1, 2, 3};
std::cout << "Size: " << vec.size() << std::endl;       // 输出: 3
std::cout << "Capacity: " << vec.capacity() << std::endl; // 输出: 3
std::cout << "Is empty? " << (vec.empty() ? "Yes" : "No") << std::endl; // 输出: No

可以使用 resize、reserve、shrink_to_fit 调整向量的大小。

// 辅助函数，用于输出 vector 的大小和容量
void printVectorInfo(const std::vector<int>& vec, const std::string& message) {
    std::cout << message << std::endl;
    std::cout << "大小: " << vec.size() << ", 容量: " << vec.capacity() << std::endl;
}

std::vector<int> vec;
printVectorInfo(vec, "初始状态:"); // 大小: 0, 容量: 0
// 使用 reserve 预留空间
vec.reserve(20);
printVectorInfo(vec, "使用 reserve(20) 后:"); // 大小: 0, 容量: 20
// 使用 resize 增加元素数量
vec.resize(10);
printVectorInfo(vec, "使用 resize(10) 后:"); // 大小: 10, 容量: 20
// 输出元素值（默认初始化为 0）
std::cout << "resize(10) 后的元素值: ";
for (int num : vec) {
    std::cout << num << " ";
}
std::cout << std::endl;  // resize(10) 后的元素值: 0 0 0 0 0 0 0 0 0 0 

// 使用 resize 继续增加元素数量，并指定初始化值
vec.resize(15, 5);
printVectorInfo(vec, "使用 resize(15, 5) 后:"); // 大小: 15, 容量: 20
// 输出元素值
std::cout << "resize(15, 5) 后的元素值: ";
for (int num : vec) {
    std::cout << num << " ";
}
std::cout << std::endl;  // resize(15, 5) 后的元素值: 0 0 0 0 0 0 0 0 0 0 5 5 5 5 5 

// 使用 resize 减少元素数量
vec.resize(5); 
printVectorInfo(vec, "使用 resize(5) 后:"); // 大小: 5, 容量: 20
// 输出元素值
std::cout << "resize(5) 后的元素值: ";
for (int num : vec) {
    std::cout << num << " ";
}
std::cout << std::endl; // resize(5) 后的元素值: 0 0 0 0 0 

// 使用 shrink_to_fit 收缩容量以匹配当前大小
vec.shrink_to_fit();
printVectorInfo(vec, "使用 shrink_to_fit() 后:"); // 大小: 5, 容量: 5

resize(count) 改变 std::vector 中的元素数量，如果不指定元素值会默认添加 0
- 若 count 大于当前大小，会在容器末尾添加新元素，可能会导致内存重新分配。
- 若 count 小于当前大小，会移除容器末尾的元素，不会改变容量。
reserve(new_cap ) 为 std::vector 预留一定的内存空间，改变容器的容量，但不会改变容器中元素的数量，数量仍旧是之前的
- 若 new_cap 大于当前容量，会重新分配内存，将原有元素复制（或移动）到新的内存空间，释放旧内存，容器容量变为 new_cap
- 若 new_cap 小于或等于当前容量，不会进行内存重新分配，容器容量保持不变。
shrink_to_fit用于释放多余的内存，使容器的容量尽可能接近当前大小

注意：reserve() 是改变容器容量，而 reverse() 是颠倒容器元素

2.2.2 添加和删除

vector 不能在首部添加元素，因为vector的内存是连续的内存空间，不能再头部额外分配内存添加元素，只能在尾部添加。如若要在头部添加元素，则需要把现有的元素整体往后移动一位，时间复杂度是O(n)，效率太低。

push_back()：在向量末尾添加一个元素，在外面构造好之后然后左值拷贝进去，右值移动进去
emplace_back()：在向量末尾添加一个元素，直接在容器内构造
pop_back()：删除向量末尾的一个元素。
insert()：在指定位置插入元素。
erase()：移除指定位置的元素或范围内的元素。
clear()：移除所有元素。

std::vector<int> vec;
// 使用push_back添加元素
vec.push_back(10);
vec.emplace_back(20);
vec.emplace_back(30);
std::cout << "After push_back: "; // 10 20 30 
for(auto num : vec) {
    std::cout << num << " ";
}

// 使用pop_back移除最后一个元素
vec.pop_back();
std::cout << "After pop_back: ";
for(auto num : vec) {
    std::cout << num << " ";
}
std::cout << std::endl; // 输出: 10 20 

// 在第二个位置插入25
vec.insert(vec.begin() + 1, 25);
std::cout << "After insert: ";
for(auto num : vec) {
    std::cout << num << " ";
}
std::cout << std::endl; // 输出: 10 25 20 

// 删除第二个元素（25）
vec.erase(vec.begin() + 1);
std::cout << "After erase: ";
for(auto num : vec) {
    std::cout << num << " ";
}
std::cout << std::endl; // 输出: 10 20 

// 清空向量
vec.clear();
std::cout << "After clear, size: " << vec.size() << std::endl; // 输出: 0

2.2.3 访问

operator[]：通过索引访问元素。
at()：通过索引访问元素，带边界检查。
front()：访问第一个元素。
back()：访问最后一个元素。

std::vector<std::string> fruits = {"Apple", "Banana", "Cherry"};
// 使用operator[]访问元素
std::cout << "First fruit: " << fruits[0] << std::endl; // 输出: Apple
// 使用at()访问元素
try {
    std::cout << "Second fruit: " << fruits.at(1) << std::endl; // 输出: Banana
    std::cout << "Invalid fruit: " << fruits.at(5) << std::endl; // 抛出异常
}
catch(const std::out_of_range& e) {
    std::cerr << "Exception: " << e.what() << std::endl;
}
// 使用front()和back()
std::cout << "Front: " << fruits.front() << std::endl; // 输出: Apple
std::cout << "Back: " << fruits.back() << std::endl;   // 输出: Cherry

2.2.4 遍历

C++ 新特性
迭代器

std::vector<int> numbers = {1, 2, 3, 4, 5};
for(auto num : numbers) {
    std::cout << num << " ";
}
for(auto it = numbers.begin(); it != numbers.end(); ++it) {
	std::cout << *it << " ";
}

2.2.5 vector修改

修改内存：

使用 reserve() 可以提前为向量分配足够的内存，减少内存重新分配的次数，提高性能。
使用 shrink_to_fit() 可以请求收缩向量的容量以匹配其大小，释放多余的内存。

修改元素：

通过索引或at()修改
使用 assign() 重新赋值
替换整个向量内容

std::vector<int> vec = {10, 20, 30, 40, 50};
// 通过索引修改元素
vec[2] = 35;
// 使用 at() 修改元素
vec.at(4) = 55;  // 10 20 35 40 55
// 使用assign修改
vec.assign(5, 10);  // 10 10 10 10 10
vec.assign({4, 5, 6}); // 4 5 6
std::vector<int> vec2 = {4, 5, 6, 7};
vec.assign(vec2.begin() + 1, vec2.end()); // 5 6 7

2.3 常用算法

2.3.1 排序

可以使用 <algorithm> 头文件中的 sort() 函数对向量进行升序降序：

std::vector<int> numbers = {50, 20, 40, 10, 30};
// 使用sort()排序，升序
std::sort(numbers.begin(), numbers.end());
// 排序后
std::cout << "After sorting: ";
for(auto num : numbers) {
    std::cout << num << " ";
}
std::cout << std::endl; // After sorting: 10 20 30 40 50 

// 使用sort()并传入lambda表达式进行降序排序
std::sort(numbers.begin(), numbers.end(), [](int a, int b) {
	return a > b;
});
//After sorting in descending order: 50 40 30 20 10

2.3.2 反转reverse()

使用 reverse() 函数可以反转向量中的元素顺序。

std::vector<char> letters = {'A', 'B', 'C', 'D', 'E'};
// 反转向量
std::reverse(letters.begin(), letters.end());
std::cout << "After reversing: ";
for(auto c : letters) {
    std::cout << c << " ";
}
std::cout << std::endl; // After reversing: E D C B A

2.3.3 查找find()

string 的 find 有四种，但是返回索引，而 vector 返回的是 iterator。但我们可以通过 std::distance 间接求得索引值。

std::vector<std::string> fruits = {"Apple", "Banana", "Cherry", "Date"};
std::string target = "Cherry";
// 使用find()查找元素
auto it = std::find(fruits.begin(), fruits.end(), target);
if(it != fruits.end()) {
    std::cout << target << " found at position " << std::distance(fruits.begin(), it) << std::endl;
}
else {
    std::cout << target << " not found." << std::endl;
}

std::distance(fruits.begin(), it) 用于求两个迭代器之间的长度。

3. list

list是一个实现了双向链表的数据结构，适合在容器中间频繁插入和删除元素。与vector不同，list不支持随机访问，但在任何位置的插入和删除操作都是常数时间。list 是离散的，不像 vector 一样是连续的。

3.1 初始化

list<int> lt1; //构造int类型的空容器
list<int> lt2(10, 2); //构造含有10个2的int类型容器
list<int> lt3(lt2); //拷贝构造int类型的lt2容器的复制品
list<int> lt{ 1,2,3,4,5 };  // 直接使用花括号进行构造---C++11允许

string s("hello world");
list<char> lt4(s.begin(),s.end()); //构造string对象某段迭代器区间的内容

int arr[] = { 1, 2, 3, 4, 5 };
int sz = sizeof(arr) / sizeof(int);
list<int> lt5(arr, arr + sz); //构造数组某段区间的复制品  ->本质是调用迭代器区间的构造函数

3.2 list操作

3.2.1 list的大小和容量

size() 函数用于获取当前容器当中的元素个数
resize() 可以重新指定list的大小，并根据需要插入或删除list中的元素来达到指定的大小
- void resize(size_type count, const T& value = T()): 会将列表的大小调整为count。如果count大于当前列表的大小，则在列表末尾插入足够数量的值为value的元素。如果count小于当前列表的大小，则删除超出count的元素
- void resize(size_type count): 将列表的大小调整为count。如果count大于当前列表的大小，则在列表末尾插入默认构造的元素。如果count小于当前列表的大小，则删除超出count的元素。
empty() 判断list是否为空，如果为空，返回true；如果非空，返回false
clear() 用于清空容器，清空后容器的size为0，但是头节点(哨兵位)不会被清除

std::list 没有 reverse()，因为 std::list 的元素在内存中是通过节点连接起来的，每个节点包含数据以及指向前一个节点和后一个节点的指针。链表的节点在内存中可以是不连续的，每当需要插入一个新元素时，只需要动态分配一个新的节点，并将其插入到链表中合适的位置即可，不需要像 std::vector 那样重新分配一大块连续的内存空间。

3.2.2 访问

front()——访问list头元素
back()——访问list尾元素

不能像 std::vector一样可以通过 at() 和 [] 进行元素访问。

list<int> mylist {1, 2, 3, 4, 5, 6, 7, 8};
cout<< "初始化后的mylist为：";
for (auto num : mylist) {
    cout<< num<< " ";
}
int front = mylist.front();   // 1
int back = mylist.back();   // 8

若想要访问其他位置的元素，可通过迭代器来间接访问：

使用迭代器手动遍历
使用 std::advance 函数，将迭代器向前或向后移动指定的步数
使用 std::next 函数，从给定迭代器向前移动指定步数后的位置

3.2.3 常见修改操作

接口名称	接口名称
push_front	在list首元素前插入值为val的元素
pop_front	删除list中第一个元素
push_back	在list尾部插入值为val的元素
pop_back	删除list中最后一个元素
insert（⭐）	在list position 位置中插入值为val的元素
erase（⭐）	删除list position位置的元素
swap	交换两个list中的元素，`list1.swap(list2)`，两个list存储的元素类型必须相同，元素个数可以不同

这里着重学习 insert() 和 earse() 两个函数：

insert() 共有三种形式：

1
2
3

insert(iterator, value); 
insert(iterator, num, value); 
insert(iterator, iterator1, iterator2);

使用 insert(iterator,value)方法，作用是向iterator迭代器指向元素的前边添加一个元素value，并返回一个迭代器指向新插入的元素。
使用 insert(iterator,num,value)方法，作用是向iterator迭代器指向元素的前边添加num个元素value，并返回一个迭代器指向新插入的第一个元素。
使用 insert(iterator, iterator1, iterator2);方法，作用是向iterator迭代器指向元素的前边添加[iterator1,iterator2)之间的元素

// 初始化一个 list
std::list<int> myList = {1, 2, 3, 4};
// 1. insert(iterator, value);
auto it = myList.begin();
++it; // 移动到第二个元素的位置
myList.insert(it, 5);  // After insert(iterator, value): 1 5 2 3 4

// 重置 list
myList = {1, 2, 3, 4};
// 2. insert(iterator, num, value);
it = myList.begin();
++it; // 移动到第二个元素的位置
myList.insert(it, 3, 6); // After insert(iterator, num, value): 1 6 6 6 2 3 4 

// 重置 list
myList = {1, 2, 3, 4};
// 3. insert(iterator, iterator1, iterator2);
std::vector<int> vec = {7, 8, 9};
it = myList.begin();
++it; // 移动到第二个元素的位置
myList.insert(it, vec.begin(), vec.end()); // After insert(iterator, iterator1, iterator2): 1 7 8 9 2 3 4

erase() 共有两种形式：

1 2	list.erase(iterator) list.erase(iterator1,iterator2)

list.erase(iterator) 这种用法会删除迭代器iterator指向的元素，返回指向下一个元素的迭代器。
list.erase(iterator1,iterator2) 这种用法会删除迭代器iterator1指向的元素到iterator2指向元素之间的元素，包括iterator1指向的元素但不包括iterator2指向的元素，即擦除[iterator1,iterator2)，返回指向 iterator2 所指向元素的迭代器

// 初始化一个 list
std::list<int> myList = {1, 2, 3, 4, 5, 6, 7, 8};
// 1. list.erase(iterator);
auto it = myList.begin();
// 移动迭代器到第三个元素的位置
std::advance(it, 2); 
// 移除第三个元素
it = myList.erase(it);  // After list.erase(iterator): 1 2 4 5 6 7 8 

// 2. list.erase(iterator1, iterator2);
auto it1 = myList.begin();
auto it2 = myList.begin();
// 移动 it1 到第二个元素的位置
std::advance(it1, 1); 
// 移动 it2 到第五个元素的位置
std::advance(it2, 4); 
// 移除 [it1, it2) 范围内的元素
it2 = myList.erase(it1, it2);  // After list.erase(iterator1, iterator2): 1 6 7 8

3.2.4 常见操作函数

接口名称	接口名称
splice	将元素从列表转移到其它列表
remove	删除具有特定值的元素
remove_if	删除满足条件的元素
unique	删除重复值
sort	容器中的元素排序
merge	合并排序列表
reverse	反转元素的顺序

std::vector 中没有 sort()、reverse() 成员函数，但可以通过 std:: 的算法 std::sort()、std::reverse() 实现，而list中有 sort()、reverse() 成员函数

a）splice()

splice共有三种形式，分别为：

splice(iterator_pos, otherList) : 将otherList中的所有元素移动到iterator_pos指向元素之前
splice(iterator_pos, otherList, iter1): 从 otherList转移 iter1 指向的元素到当前list。元素被插入到 iterator_pos指向的元素之前。
splice(iterator_pos, otherList, iter_start, iter_end) : 从 otherList转移范围 [iter_start, iter_end) 中的元素到当前列表。元素被插入到 iterator_pos指向的元素之前。

// 创建两个 std::list 容器
std::list<int> list1 = {1, 2, 3};
std::list<int> list2 = {4, 5, 6};

// 1. splice(iterator_pos, otherList)
// 将 list2 中的所有元素移动到 list1 中第二个元素之前
auto it1 = std::next(list1.begin());
list1.splice(it1, list2);
// list1: 1 4 5 6 2 3 
// list2: 

// 重置 list1 和 list2
list1 = {1, 2, 3};
list2 = {4, 5, 6};
// 2. splice(iterator_pos, otherList, iter1)
// 从 list2 转移第二个元素到 list1 中第二个元素之前
auto it2 = std::next(list1.begin());
auto it3 = std::next(list2.begin());
list1.splice(it2, list2, it3);
// list1: 1 5 2 3
// list2: 4 6 

// 重置 list1 和 list2
list1 = {1, 2, 3};
list2 = {4, 5, 6};
// 3. splice(iterator_pos, otherList, iter_start, iter_end)
// 从 list2 转移范围 [第二个元素, 最后一个元素) 中的元素到 list1 中第二个元素之前
auto it4 = std::next(list1.begin());
auto start = std::next(list2.begin());
auto end = list2.end();
list1.splice(it4, list2, start, end);
// list1: 1 5 6 2 3 
// list2: 4

b）remove

std::list 的 remove 方法用于从列表中移除与指定值相等的元素

1
2
3

std::list<int> mylist {1, 2, 3, 4, 5};
// 移除列表中所有值为2的元素
mylist.remove(2); // 1 3 4 5

c）remove_if()——移除满足特定标准的元素

bool isEven(int n) {
    return n % 2 == 0;
}

std::list<int> mylist {1, 2, 3, 4, 5};
// 移除列表中所有满足 isEven 的元素（偶数）
mylist.remove_if(isEven); // 1 3 5

d）unique()——删除连续的重复元素

unique()方法用于移除链表中相邻且重复的元素，仅保留一个副本。

1 2	std::list<int> myList = {1, 2, 2, 3, 3, 4, 5, 5, 5}; myList.unique(); // 1 2 3 4 5

e）sort()——对元素进行排序

sort()方法用于对链表中的元素进行排序。默认情况下，它按升序对元素进行排序，使用元素类型的 < 运算符进行比较。

// 自定义比较函数，用于降序排序
bool compareDesc(int a, int b) {
    return a > b;
}

std::list<int> myList = {5, 3, 2, 4, 1};
myList.sort(); // 1 2 3 4 5 
myList.sort(compareDesc); // 5 4 3 2 1

f）merge()——合并list

merge()方法将另一个列表的元素插入到调用方法的列表中，并保持排序顺序

注意：merge()方法只能用于已排序的list。如果list未排序，则合并的结果将是不正确的。

std::list<int> list1 = {1, 3, 5};
std::list<int> list2 = {2, 4, 6};
// 将 list2 合并到 list1 中
list1.merge(list2); // 1 2 3 4 5 6

g）reverse()——将该链表的所有元素的顺序反转

reverse()方法用于反转链表中元素的顺序，即将链表中的第一个元素变为最后一个元素，第二个元素变为倒数第二个元素，以此类推

1 2	std::list<int> myList = {1, 2, 3, 4, 5}; myList.reverse(); // 5 4 3 2 1

h）assign()——将值赋给容器

assign()方法用于将链表中的元素替换为新的元素序列。它可以接受不同形式的参数，提供了两种重载形式。

第一种形式接受迭代器范围作为参数，用于将另一个容器或数组中的元素复制到链表中。它会将链表清空，并将指定范围内的元素复制到链表中。void assign(InputIterator first, InputIterator last);
第二种形式接受一个元素数量和一个值作为参数，用于将指定数量的相同值的元素分配给链表。它会将链表清空，并将指定数量的元素赋值为指定的值。void assign(size_type count, const T& value);

// 创建一个空的 std::list
std::list<int> myList;
// 第一种形式：使用迭代器范围进行赋值
std::vector<int> myVector = {1, 2, 3, 4, 5};
myList.assign(myVector.begin(), myVector.end()); // 1 2 3 4 5 

// 清空列表，为下一次赋值做准备
myList.clear();
// 第二种形式：使用元素数量和值进行赋值
myList.assign(3, 10); // 10 10 10

4. deque

deque（双端队列）是一种支持在两端高效插入和删除元素的序列容器。与vector相比，deque支持在前端和后端均以常数时间进行插入和删除操作。

deque通常由一系列固定大小的数组块组成，这些块通过一个中央映射数组进行管理。这种结构使得在两端扩展时不需要重新分配整个容器的内存，从而避免了vector在前端插入的高成本。

4.1 初始化

std::deque<int> myDeque;
std::deque<int> d(10); // 创建一个具有 n 个元素的 deque 容器，默认为0。 0 0 0 0 0 0 0 0 0 0 
std::deque<int> myDeque(5, 10); // 10 10 10 10 10
std::deque<int> myDeque = {1, 3, 5, 7, 9}; // 1 3 5 7 9

std::deque<int> d1(5);
std::deque<int> d2(d1); // 5

std::vector<int> myVector = {1, 2, 3, 4, 5};
// 注意，采用此方式，必须保证新旧容器存储的元素类型一致。
std::deque<int> myDeque(myVector.begin(), myVector.end()); // 1 2 3 4 5

// 通过拷贝其他类型容器中指定区域内的元素（也可以是普通数组），元素类型要相同
//拷贝普通数组，创建deque容器
int a[] = { 1,2,3,4,5 };
std::deque<int>d(a, a + 5);
//适用于所有类型的容器
std::array<int, 5>arr{ 11,12,13,14,15 };
std::deque<int>d(arr.begin()+2, arr.end());//拷贝arr容器中的{13,14,15}

4.2 成员函数

函数成员	函数功能
begin()	返回指向容器中第一个元素的迭代器。
end()	返回指向容器最后一个元素所在位置后一个位置的迭代器，通常和 begin() 结合使用。
rbegin()	返回指向最后一个元素的迭代器。
rend()	返回指向第一个元素所在位置前一个位置的迭代器。
cbegin()	和 begin() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
cend()	和 end() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
crbegin()	和 rbegin() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
crend()	和 rend() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改元素。
size()	返回实际元素个数。
max_size()	返回容器所能容纳元素个数的最大值。这通常是一个很大的值，一般是 2^32-1，我们很少会用到这个函数。
resize()	改变实际元素的个数，若大于size()，则插入指定元素，默认0；若小于size()，删除末尾的元素
empty()	判断容器中是否有元素，若无元素，则返回 true；反之，返回 false。
shrink _to_fit()	将内存减少到等于当前元素实际所使用的大小。
at()	使用经过边界检查的索引访问元素。
[]	支持索引访问，不进行边界检查，如果索引越界，会抛出 `std::out_of_range` 异常。范围从0~deque.size() - 1
front()	返回第一个元素的引用。
back()	返回最后一个元素的引用。
assign()	用新元素替换原有内容。
push_back()	在序列的尾部添加一个元素。
push_front()	在序列的头部添加一个元素。
pop_back()	移除容器尾部的元素。
pop_front()	移除容器头部的元素。
insert()	在指定的位置插入一个或多个元素。
erase()	移除一个元素或一段元素。
clear()	移出所有的元素，容器大小变为 0。
swap()	交换两个容器的所有元素。
emplace()	在指定的位置直接生成一个元素
emplace_front()	在容器头部生成一个元素。和 push_front() 的区别是，该函数直接在容器头部构造元素，省去了复制移动元素的过程。
emplace_back()	在容器尾部生成一个元素。和 push_back() 的区别是，该函数直接在容器尾部构造元素，省去了复制移动元素的过程。

和 vector 相比，额外增加了实现在容器头部添加和删除元素的成员函数，同时删除了 capacity()、reserve() 成员函数。

std::deque 采用分段连续存储的方式，它会根据需要动态地分配和释放内存块，不需要一次性分配一大块连续的内存。因此，std::deque 没有 capacity() 和 reserve() 成员函数。当需要添加元素时，std::deque 会在合适的内存块上进行操作，或者在必要时分配新的内存块，而不需要预先分配大量的内存。

5. 三种序列式容器的特点

特性	`vector`	`deque`	`list`
内存结构	单一连续内存块	多块连续内存，通过映射数组管理	双向链表
随机访问	是，常数时间（O(1)）	是，常数时间（O(1)）	否，需要线性时间（O(n)）
前端插入/删除	低效，线性时间（O(n)）	高效，常数时间（O(1)）	高效，常数时间（O(1)）
末端插入/删除	高效，常数时间（O(1)）	高效，常数时间（O(1)）	高效，常数时间（O(1)）
内存碎片	低，由于单一连续内存块	较高，由于多块内存管理	较高，由于节点分散在内存中
元素隔离	高，局部性较好	中等，分块存储提高了部分局部性	低，元素分散存储，缓存效率低
应用场景	需要频繁随机访问、末端操作的场景	需要频繁在两端插入/删除且可以随机访问的场景	需要频繁在中间插入/删除且不需要随机访问的场景

6. map、unordered_map

map是一个关联容器，用于存储键值对（key-value）。它基于键自动排序，且每个键都是唯一的，且存储后不能被修改。map提供了快速的查找、插入和删除操作。通常使用自平衡的二叉搜索树（如红黑树、AVL树）实现。这确保了所有操作的时间复杂度为对数时间（O(log n)），且元素按照键的顺序排列。
unordered_map也是一种关联容器，用于存储键值对，但它不保证元素的顺序。unordered_map基于哈希表实现，提供了平均常数时间（O(1)）的查找、插入和删除操作。

在使用 unordered_map 和 unordered_set 时需注意，我们不能使用哈希表实现的无序map或者set存储标准库不提供默认哈希函数的类型，比如：自定义类型（自定义的类、结构体）、复合类型（std::pair、std::tuple）；但我们可以存储：所有整数类型、浮点类型、指针类型（尽管我们不能直接存储自定义类型，但可以将其指针存进来）、string。

而 map 和 set 基于红黑树实现，只能存储支持比较操作 operator< 的类型，并且可复制和可移动。

对比：

操作	`map`	`unordered_map`
查找	`O(log n)`	平均 `O(1)`
插入	`O(log n)`	平均 `O(1)`
删除	`O(log n)`	平均 `O(1)`
内存使用	较高	较低
元素顺序	有序	无序
使用场景	需要按键的顺序遍历元素需要有序的关联数组需要高效的范围查找	对元素顺序没有要求需要极高效的查找、插入和删除操作不需要自定义的排序规则

6.1 map 初始化

map 容器的模板定义如下：

template < class Key,                                     // 指定键（key）的类型
           class T,                                       // 指定值（value）的类型
           class Compare = less<Key>,                     // 指定排序规则
           class Alloc = allocator<pair<const Key,T> >    // 指定分配器对象的类型
           > class map;

可以看到，map 容器模板有 4 个参数，其中后 2 个参数都设有默认值。大多数场景中，我们只需要设定前 2 个参数的值，有些场景可能会用到第 3 个参数，但最后一个参数几乎不会用到。

map 容器的模板类中包含多种构造函数，因此创建 map 容器的方式也有多种，下面就几种常用的创建 map 容器的方法，做一一讲解。

通过调用 map 容器类的默认构造函数，可以创建出一个空的 map 容器，比如：

1	std::map<std::string, int>myMap;

通过此方式创建出的 myMap 容器，初始状态下是空的，即没有存储任何键值对。鉴于空 map 容器可以根据需要随时添加新的键值对，因此创建空 map 容器是比较常用的。

当然在创建 map 容器的同时，也可以通过列表初始化进行初始化，比如：

1	std::map<std::string, int>myMap{ {"C语言教程",10},{"STL教程",20} };

由此，myMap 容器在初始状态下，就包含有 2 个键值对。

再次强调，map 容器中存储的键值对，其本质都是 pair 类模板创建的 pair 对象。因此，下面程序也可以创建出一模一样的 myMap 容器：

1	std::map<std::string, int>myMap{std::make_pair("C语言教程",10),std::make_pair("STL教程",20)};

除此之外，在某些场景中，可以利用先前已创建好的 map 容器，再创建一个新的 map 容器。例如：

1	std::map<std::string, int>newMap(myMap);

由此，通过调用 map 容器的拷贝构造函数，即可成功创建一个和 myMap 完全一样的 newMap 容器。

C++ 11 标准中，还为 map 容器增添了移动构造函数。当有临时的 map 对象作为参数，传递给要初始化的 map 容器时，此时就会调用移动构造函数。举个例子：

1 2	//调用 map 类模板的移动构造函数创建 newMap 容器 std::map<std::string, int>newMap(std::move(MyMap));

注意，无论是调用复制构造函数还是调用拷贝构造函数，都必须保证这 2 个容器的类型完全一致。

map 类模板还支持取已建 map 容器中指定区域内的键值对，创建并初始化新的 map 容器。例如：

1 2	std::map<std::string, int>myMap{ {"C语言教程",10},{"STL教程",20} }; std::map<std::string, int>newMap(++myMap.begin(), myMap.end());

这里，通过调用 map 容器的双向迭代器，实现了在创建 newMap 容器的同时，将其初始化为仅包含一个 {“STL教程”,20} 键值对的容器。

当然，在以上几种创建 map 容器的基础上，我们都可以手动修改 map 容器的排序规则。默认情况下，map 容器调用 std::less<T> 规则，根据容器内各键值对的键的大小，对所有键值对做升序排序。因此，如下 2 行创建 map 容器的方式，其实是等价的：

1 2	std::map<std::string, int>myMap{ {"C语言教程",10},{"STL教程",20} }; std::map<std::string, int, std::less<std::string> >myMap{ {"C语言教程",10},{"STL教程",20} };

以上 2 中创建方式生成的 myMap 容器，其内部键值对排列的顺序为：

<”C语言教程”, 10>
<”STL教程”, 20>

下面程序手动修改了 myMap 容器的排序规则，令其作降序排序：

1	std::map<std::string, int, std::greater<std::string> >myMap{ {"C语言教程",10},{"STL教程",20} };

此时，myMap 容器内部键值对排列的顺序为：

<”STL教程”, 20>
<”C语言教程”, 10>

6.2 map 成员方法

成员方法	功能
begin()	返回指向容器中第一个（注意，是已排好序的第一个）键值对的双向迭代器。如果 map 容器用 const 限定，则该方法返回的是 const 类型的双向迭代器。
end()	返回指向容器最后一个元素（注意，是已排好序的最后一个）所在位置后一个位置的双向迭代器，通常和 begin() 结合使用。如果 map 容器用 const 限定，则该方法返回的是 const 类型的双向迭代器。
rbegin()	回指向最后一个（注意，是已排好序的最后一个）元素的反向双向迭代器。如果 map 容器用 const 限定，则该方法返回的是 const 类型的反向双向迭代器。
rend()	返回指向第一个（注意，是已排好序的第一个）元素所在位置前一个位置的反向双向迭代器。如果 map 容器用 const 限定，则该方法返回的是 const 类型的反向双向迭代器。
cbegin()	和 begin() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改容器内存储的键值对。
cend()	和 end() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改容器内存储的键值对。
crbegin()	和 rbegin() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改容器内存储的键值对。
crend()	和 rend() 功能相同，只不过在其基础上，增加了 const 属性，不能用于修改容器内存储的键值对。
find(key)	在 map 容器中查找键为 key 的键值对，如果成功找到，则返回指向该键值对的双向迭代器；反之，则返回和 end() 方法一样的迭代器。另外，如果 map 容器用 const 限定，则该方法返回的是 const 类型的双向迭代器。
lower_bound(key)	返回一个指向当前 map 容器中第一个大于或等于 key 的键值对的双向迭代器。如果 map 容器用 const 限定，则该方法返回的是 const 类型的双向迭代器。
upper_bound(key)	返回一个指向当前 map 容器中第一个大于 key 的键值对的迭代器。如果 map 容器用 const 限定，则该方法返回的是 const 类型的双向迭代器。
equal_range(key)	该方法返回一个 pair 对象（包含 2 个双向迭代器），其中 pair.first 和 lower_bound() 方法的返回值等价，pair.second 和 upper_bound() 方法的返回值等价。也就是说，该方法将返回一个范围，该范围中包含的键为 key 的键值对（map 容器键值对唯一，因此该范围最多包含一个键值对）。
empty()	若容器为空，则返回 true；否则 false。
size()	返回当前 map 容器中存有键值对的个数。
max_size()	返回 map 容器所能容纳键值对的最大个数，不同的操作系统，其返回值亦不相同。
operator[]	map容器重载了 [] 运算符，只要知道 map 容器中某个键值对的键的值，就可以向获取数组中元素那样，通过键直接获取对应的值。我们也可以通过 [] 来添加键值对。如果键已经存在，会修改对应的值；若键不存在，则可以使用 [] 运算符插入或修改键值对。
at(key)	找到 map 容器中 key 键对应的值，如果找不到，该函数会引发 out_of_range 异常。
insert()	向 map 容器中插入键值对。`myMap.insert(std::make_pair("banana", 2));`、`myMap.insert({ "cherry", 3 });`
erase()	删除 map 容器指定位置、指定键（key）值或者指定区域内的键值对。
swap()	交换 2 个 map 容器中存储的键值对，这意味着，操作的 2 个键值对的类型必须相同。
clear()	清空 map 容器中所有的键值对，即使 map 容器的 size() 为 0。
emplace()	在当前 map 容器中的指定位置处构造新键值对。其效果和插入键值对一样，但效率更高。`emplace` 方法返回一个 `std::pair`，其中 `first` 是一个迭代器，指向插入的元素或者已经存在的具有相同键的元素；`second` 是一个布尔值，表示是否成功插入了新元素（如果键已经存在，则插入失败，`second` 为 `false`；否则，插入成功，`second` 为 `true`）。
emplace_hint()	在本质上和 emplace() 在 map 容器中构造新键值对的方式是一样的，不同之处在于，使用者必须为该方法提供一个指示键值对生成位置的迭代器，并作为该方法的第一个参数。
count(key)	在当前 map 容器中，查找键为 key 的键值对的个数并返回。注意，由于 map 容器中各键值对的键的值是唯一的，因此该函数的返回值最大为 1。

6.3 unordered_map 初始化

unordered_map 容器模板的定义如下所示：

template < class Key,                        //键值对中键的类型
           class T,                          //键值对中值的类型
           class Hash = hash<Key>,           //容器内部存储键值对所用的哈希函数
           class Pred = equal_to<Key>,       //判断各个键值对键相同的规则
           class Alloc = allocator< pair<const Key,T> >  // 指定分配器对象的类型
           > class unordered_map;

以上 5 个参数中，必须显式给前 2 个参数传值，并且除特殊情况外，最多只需要使用前 4 个参数，各自的含义和功能如下表所示。

参数	含义
`<key,T>`	前 2 个参数分别用于确定键值对中键和值的类型，也就是存储键值对的类型。
`Hash = hash<Key>`	用于指明容器在存储各个键值对时要使用的哈希函数，默认使用 STL 标准库提供的 `hash<key>` 哈希函数。注意，默认哈希函数只适用于基本数据类型（包括 string 类型），而不适用于自定义的结构体或者类。
`Pred = equal_to<Key>`	要知道，`unordered_map` 容器中存储的各个键值对的键是不能相等的，而判断是否相等的规则，就由此参数指定。默认情况下，使用 STL 标准库中提供的 `equal_to<key>` 规则，该规则仅支持可直接用 `==` 运算符做比较的数据类型。

总的来说，当无序容器中存储键值对的键为自定义类型时，默认的哈希函数 hash 以及比较函数 equal_to 将不再适用，只能自己设计适用该类型的哈希函数和比较函数，并显式传递给 Hash 参数和 Pred 参数。

常见的创建 unordered_map 容器的方法有以下几种。

通过调用 unordered_map 模板类的默认构造函数，可以创建空的 unordered_map 容器。比如：

1	std::unordered_map<std::string, std::string> umap;

由此，就创建好了一个可存储 <string,string> 类型键值对的 unordered_map 容器。

当然，在创建 unordered_map 容器的同时，可以完成初始化操作。比如：

std::unordered_map<std::string, std::string> umap{
    {"Python教程","http://c.biancheng.net/python/"},
    {"Java教程","http://c.biancheng.net/java/"},
    {"Linux教程","http://c.biancheng.net/linux/"} };

通过此方法创建的 umap 容器中，就包含有 3 个键值对元素。

另外，还可以调用 unordered_map 模板中提供的复制（拷贝）构造函数，将现有 unordered_map 容器中存储的键值对，复制给新建 unordered_map 容器。例如，在第二种方式创建好 umap 容器的基础上，再创建并初始化一个 umap2 容器：

1	std::unordered_map<std::string, std::string> umap2(umap);

由此，umap2 容器中就包含有 umap 容器中所有的键值对。

除此之外，C++ 11 标准中还向 unordered_map 模板类增加了移动构造函数，即以右值引用的方式将临时 unordered_map 容器中存储的所有键值对，全部复制给新建容器。例如：

//返回临时 unordered_map 容器的函数
std::unordered_map <std::string, std::string > retUmap(){
    std::unordered_map<std::string, std::string>tempUmap{
        {"Python教程","http://c.biancheng.net/python/"},
        {"Java教程","http://c.biancheng.net/java/"},
        {"Linux教程","http://c.biancheng.net/linux/"} };
    return tempUmap;
}
//调用移动构造函数，创建 umap2 容器
std::unordered_map<std::string, std::string> umap2(retUmap());

注意，无论是调用复制构造函数还是拷贝构造函数，必须保证 2 个容器的类型完全相同。

当然，如果不想全部拷贝，可以使用 unordered_map 类模板提供的迭代器，在现有 unordered_map 容器中选择部分区域内的键值对，为新建 unordered_map 容器初始化。例如：

1 2	//传入 2 个迭代器， std::unordered_map<std::string, std::string> umap2(++umap.begin(),umap.end());

通过此方式创建的 umap2 容器，其内部就包含 umap 容器中除第 1 个键值对外的所有其它键值对。

6.4 unordered_map 成员方法

unordered_map 既可以看做是关联式容器，更属于自成一脉的无序容器。因此在该容器模板类中，既包含一些在学习关联式容器时常见的成员方法，还有一些属于无序容器特有的成员方法。

成员方法	功能
begin()	返回指向容器中第一个键值对的正向迭代器。
end()	返回指向容器中最后一个键值对之后位置的正向迭代器。
cbegin()	和 begin() 功能相同，只不过在其基础上增加了 const 属性，即该方法返回的迭代器不能用于修改容器内存储的键值对。
cend()	和 end() 功能相同，只不过在其基础上，增加了 const 属性，即该方法返回的迭代器不能用于修改容器内存储的键值对。
empty()	若容器为空，则返回 true；否则 false。
size()	返回当前容器中存有键值对的个数。
max_size()	返回容器所能容纳键值对的最大个数，不同的操作系统，其返回值亦不相同。
operator[key]	该模板类中重载了 [] 运算符，其功能是可以向访问数组中元素那样，只要给定某个键值对的键 key，就可以获取该键对应的值。注意，如果当前容器中没有以 key 为键的键值对，则其会使用该键向当前容器中插入一个新键值对。
at(key)	返回容器中存储的键 key 对应的值，如果 key 不存在，则会抛出 out_of_range 异常。
find(key)	查找以 key 为键的键值对，如果找到，则返回一个指向该键值对的正向迭代器；反之，则返回一个指向容器中最后一个键值对之后位置的迭代器（如果 end() 方法返回的迭代器）。
count(key)	在容器中查找以 key 键的键值对的个数。
equal_range(key)	返回一个 pair 对象，其包含 2 个迭代器，用于表明当前容器中键为 key 的键值对所在的范围。
emplace()	向容器中添加新键值对，效率比 insert() 方法高。`emplace` 方法返回一个 `std::pair`，其中 `first` 是一个迭代器，指向插入的元素或者已经存在的具有相同键的元素；`second` 是一个布尔值，表示是否成功插入了新元素（如果键已经存在，则插入失败，`second` 为 `false`；否则，插入成功，`second` 为 `true`）。
emplace_hint()	向容器中添加新键值对，效率比 insert() 方法高。
insert()	向容器中添加新键值对。
erase()	删除指定键值对。
clear()	清空容器，即删除容器中存储的所有键值对。
swap()	交换 2 个 unordered_map 容器存储的键值对，前提是必须保证这 2 个容器的类型完全相等。
bucket_count()	返回当前容器底层存储键值对时，使用桶（一个线性链表代表一个桶）的数量。
max_bucket_count()	返回当前系统中，unordered_map 容器底层最多可以使用多少桶。
bucket_size(n)	返回第 n 个桶中存储键值对的数量。
bucket(key)	返回以 key 为键的键值对所在桶的编号。
load_factor()	返回 unordered_map 容器中当前的负载因子。负载因子，指的是的当前容器中存储键值对的数量（size()）和使用桶数（bucket_count()）的比值，即 load_factor() = size() / bucket_count()。
max_load_factor()	返回或者设置当前 unordered_map 容器的负载因子。
rehash(n)	将当前容器底层使用桶的数量设置为 n。
reserve()	将存储桶的数量（也就是 bucket_count() 方法的返回值）设置为至少容纳count个元（不超过最大负载因子）所需的数量，并重新整理容器。
hash_function()	返回当前容器使用的哈希函数对象。

7. AVL实现map

7.1 基本概念

AVL 和红黑树都是一种自平衡的二叉搜索树，它们在保持二叉搜索树基本性质的同时，通过特定的平衡机制来确保树的高度始终不超过1（树上任一节点的左子树和右子树的高度之差不超过 1）.

二叉搜索树（BST）满足下列三点性质：

左子树上所有节点的关键字均小于根节点的关键字
右子树上所有节点的关键字均大于根节点的关键字
左子树和右子树又各是一颗二叉搜索树

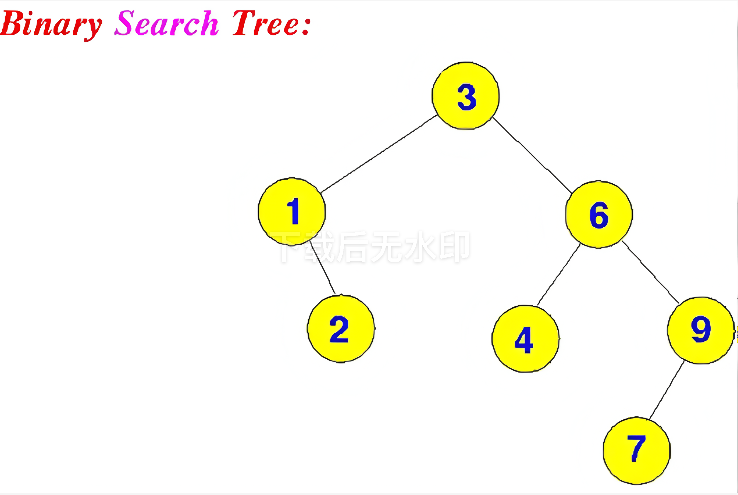
如下图所示：

二叉搜索树只需要满足：左子树节点值<根节点值<右子树节点值

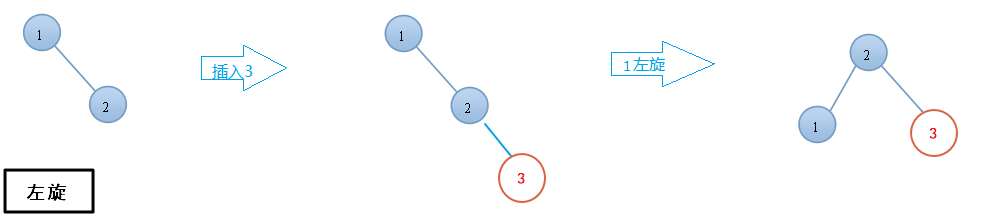
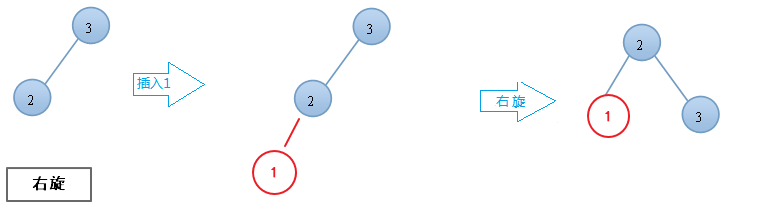
当插入或删除操作导致 AVL 树的某个节点的平衡因子超出了 -1 到 1 的范围时，AVL树实现平衡的方式是通过旋转操作：

左旋：将一个节点的右子树提升为根节点，原根节点变为新根节点的左子树。
右旋：将一个节点的左子树提升为根节点，原根节点变为新根节点的右子树。
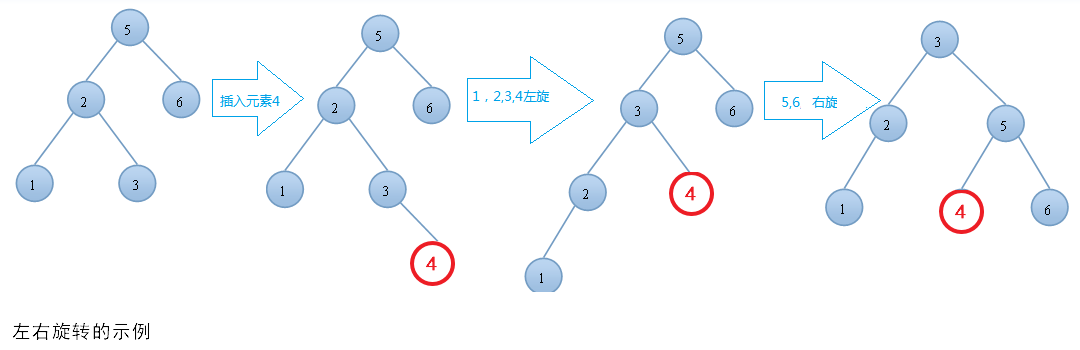
左右旋：先对左子树进行左旋，再对根节点进行右旋。
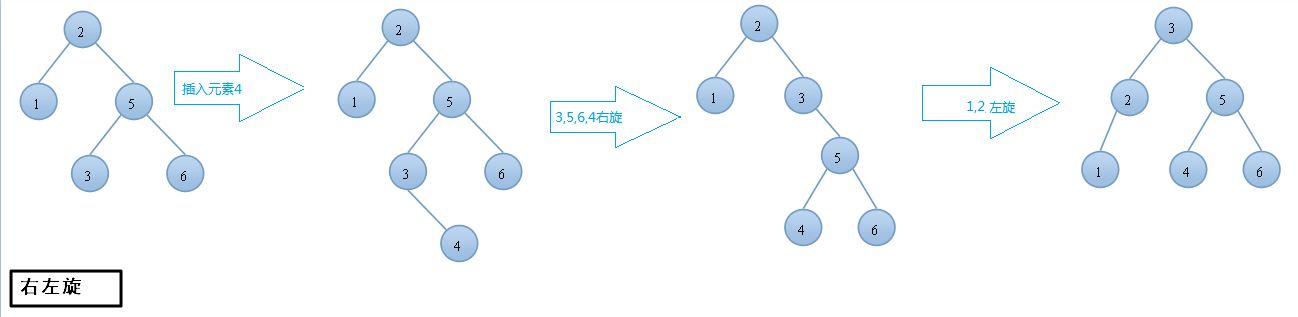
右左旋：先对右子树进行右旋，再对根节点进行左旋。

在这里插入图片描述

7.2 实现

在实现之前，必须要注意：键类型KeyType必须支持比较操作，能够使用比较运算符 opeator<。若是自定义结构，必须重载 opeator<：

struct CustomKey {
    int id;
    std::string name;

    bool operator<(const CustomKey& other) const {
        if (id != other.id)
            return id < other.id;
        return name < other.name;
    }
};

7.2.1 模板化AVL树节点

将AVLNode结构模板化，使其能够处理不同类型的键和值。假设键类型KeyType支持操作运算符operator<进行比较，因为AVL树需要对键进行排序以维护其性质。**如果自定义的键类型不支持操作运算符operator<进行比较，我们需要在该类型中重载operator<**。

首先，我们定义AVL树的节点。每个节点包含一个键（key）、一个值（value）、节点高度（height），以及指向左子节点和右子节点的指针。

#include <iostream>
#include <string>
#include <vector>
#include <algorithm> 
#include <functional> // 用于 std::function

// 模板化的AVL树节点结构
template <typename KeyType, typename ValueType>
struct AVLNode{
	KeyType _key;
	ValueType _value;
	int _height;
	AVLNode* _left, _right;

	AVLNode(const KeyType& key, const ValueType& value)
		: _key(key), _value(value), _height(1), _left(nullptr), _right(nullptr) {}
};

7.2.2 辅助函数模板化

辅助函数同样需要模板化，以适应不同的AVLNode类型。

7.2.2.1 获取节点高度

获取节点的高度。如果节点为空，则高度为0

template <typename KeyType, typename ValueType>
int getHeight(AVLNode<KeyType, ValueType>* node) {
    if (node == nullptr)
        return 0;
    return node->_height;
}

7.2.2.2 获取平衡因子

左子树高度减去右子树高度就是平衡因子

template <typename KeyType, typename ValueType>
int getBalance(AVLNode<KeyType, ValueType>* node) {
    if (node == nullptr)
        return 0;
    return getHeight(node->_left) - getHeight(node->_right);
}

7.2.2.3 右旋

右旋转用于处理左子树过高的情况

    y                             x
   / \                           / \
  x   T3            ==>         z   y
 / \                               / \
z   T2                            T2  T3

template <typename KeyType, typename ValueType>
AVLNode<KeyType, ValueType>* rightRotate(AVLNode<KeyType, ValueType>* y) {
    AVLNode<KeyType, ValueType>* x = y->_left;
    AVLNode<KeyType, ValueType>* T2 = x->_right;
    // 执行旋转
    x->_right = y;
    y->_left = T2;
    // 更新高度
    y->_height = std::max(getHeight(y->_left), getHeight(y->_right)) + 1;
    x->_height = std::max(getHeight(x->_left), getHeight(x->_right)) + 1;
    // 返回新的根
    return x;
}

7.2.2.4 左旋

左旋转用于处理右子树过高的情况

  x                             y
 / \                           / \
T1  y           ==>           x   z
   / \                       / \
  T2  z                     T1  T2

template <typename KeyType, typename ValueType>
AVLNode<KeyType, ValueType>* leftRotate(AVLNode<KeyType, ValueType>* x) {
    AVLNode<KeyType, ValueType>* y = x->_right;
    AVLNode<KeyType, ValueType>* T2 = y->_left;
    // 执行旋转
    y->_left = x;
    x->_right = T2;
    // 更新高度
    x->_height = std::max(getHeight(x->_right), getHeight(x->_left)) + 1;
    y->_height = std::max(getHeight(y->_right), getHeight(y->_left)) + 1;
    // 返回新的根
    return y;
}

7.2.3 AVL树的核心操作模板化

7.2.3.1 节点插入

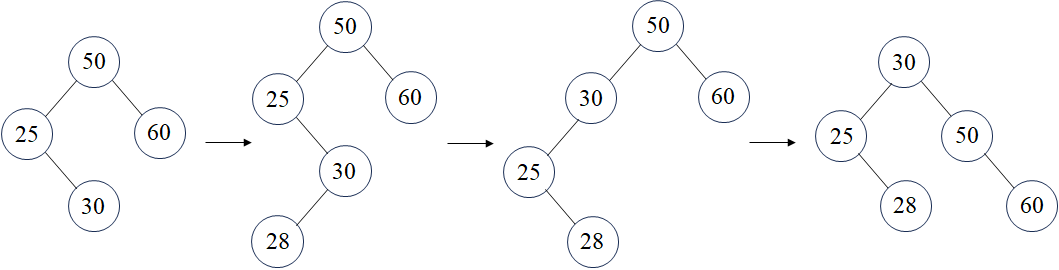
插入操作遵循标准的二叉搜索树插入方式，然后通过旋转保持树的平衡。如果插入一个新节点，可能会遇到以下情况：

1ecf2da7d4965c401f02c8c7d112971

如果插入 28，就需要我们将插入后的树先进行左旋，然后右旋，当然还可能有其他情况。

AVLNode<KeyType, ValueType>* insertNode(AVLNode<KeyType, ValueType>* node, // 当前节点
    const KeyType& key, const ValueType& value) {
    // 执行BST的插入，递归调用
    if (node ==nullptr) // 当执行到最后一层时，才会将节点插入至 nullptr 的位置
        return new AVLNode<KeyType, ValueType>(key, value);

    if (key < node->_key) // 如果插入的key值小于当前节点，那么插入当前节点的左子树
        node->_left = insertNode(node->_left, key, value);
    else if(key > node->_key) // 如果插入的key值小于当前节点，那么插入当前节点的左子树
        node->_right = insertNode(node->_right, key, value);
    else { // 如果插入key值等于当前节点key值，更新值
        node->_value = value;
        return node;
    }

    // 更新节点高度
    node->_height = std::max(getHeight(node->_left), getHeight(node->_right)) + 1;

    // 获取平衡因子
    int balance = getBalance(node);

    // 根据因子情况进行旋转
    // 左左
    if (balance > 1 and key < node->_left->_key) // 若左子树高于右子树 1 单位，且插入值小于当前节点的左子树key
        return rightRotate(node);
    // 左右
    if(balance > 1 and key > node->_left->_key) // 若左子树高于右子树 1 单位，且插入值大于当前节点的左子树key
        return rightRotate(node);
    // 右左
    if (balance < -1 and key < node->_right->_key) // 若左子树低于右子树 1 单位，且插入值小于于当前节点的右子树key
        return leftRotate(node);
    // 右右
    if (balance < -1 and key < node->_right->_key) // 若左子树低于右子树 1 单位，且插入值大于于当前节点的右子树key
        return leftRotate(node);

    return node;
}

    8 (balance = 2)
   / \
  4   10
 / \
2   6
   /
  5

对于上面这种情况，插入5，满足左右，我们先要对 4 进行左旋，然后对8进行右旋

  4 (balance = -2)
 / \
2   8
   / \
  6   10
   \
    7

对于上面这种情况，插入7，满足右左，我们先要对 8 进行右旋，然后对4进行左旋

这两种情况很特殊，必须要这样操作

7.2.3.2 获取最小值节点

用于删除节点时找到中序后继。

AVLNode<KeyType, ValueType>* getMinValueNode(AVLNode<KeyType, ValueType>* node) {
    AVLNode<KeyType, ValueType>* cur = node;
    while (cur->_left != nullptr)
        cur = cur->_left;

    return cur;
}

7.2.3.3 查找给定节点的value值

按键查找节点，返回对应的值。如果键不存在，返回nullptr。

ValueType* searchNode(AVLNode<KeyType, ValueType>* node, const KeyType& key) {
    if (node == nullptr)
        return nullptr;

    if (node->_key == key)
        return &(node->_value);
    else if (key < node->_key)
        return searchNode(node->_left, key);
    else(key > node->_key)
        return searchNode(node->_right, key);
}

7.2.3.3 删除节点（BST节点删除方式）

删除操作分为三种情况：删除节点无叶子节点、有一个子节点或有两个子节点。删除后，通过旋转保持树的平衡。删除方式和BST的方式一样：

若被删除节点 z 是叶节点，则直接删除 z，不会破坏BST的性质
若节点 z 只有一颗左子树或右子树，则让 z 的子树成为 z 的父节点的子树，覆盖 z 的位置
若节点 z 有左右两颗子树，则令 z 的中序后继（或中序前驱）代替 z（仅仅是键值对代替，z 的左右子树指向仍不变），然后从BST中删除这个中序后继（中序前驱），这样就成了第一种或第二种情况

z 的中序后继：z 的右子树中最左下节点（最小），该节点一定没有左子树

z 的中序前驱：z 的左子树中最右下节点，该节点一定没有右子树

以BST方式将指定节点删除后，需要重新旋转，以保持平衡。

AVLNode<KeyType, ValueType>* deleteNode(AVLNode<KeyType, ValueType>* root, const KeyType& key) {
    // 以 BST 方式删除
    if (root == nullptr)
        return root;

    if (key < root->_key)
        root->_left = deleteNode(root->_left, key);
    else if (key > root->_key)
        root->_right = deleteNode(root->_right, key);
    else { // 找到待删节点
        // 待删除节点无子树或只有一个子树
        if (root->_left == nullptr or root->_right == nullptr) {
            AVLNode<KeyType, ValueType>* temp = root->_left != nullptr ? root->_left : root->_right;
            // 若 temp 为空，说明待删除节点没有子节点
            if (temp == nullptr) {
                temp = rooot;
                root = nullptr; // 因为待删除节点没有子节点可以直接将待删除节点清空
            }
            else { // 待删除节点有一个子树
                *root = *temp; // 直接将待删除节点的子树复制到待删除节点的位置，相当于删除了待删除节点
            }

            delete temp;
        }
        else { // 待删除节点的左右子树都存在（难点）
            // 获取中序后继
            AVLNode<KeyType, ValueType>* temp = getMinValueNode(root->right);
            // 保持待删除节点的左右子树不变，复制中序后继的键值对到此节点
            root->key = temp->key;
            root->value = temp->value;
            // 删除中序后继（同样会判断中序后继是否有左右子树）
            root->right = deleteNode(root->right, temp->key);
        }
    }

    // 若节点删除完之后，整个树为空，则不需要旋转保持平衡
    if (root == nullptr)
        return root;

    // 更新高度
    root->_height = std::max(getHeight(root->_right), getHeight(root->_left)) + 1;
    // 获取平衡因子
    int balance = getBalance(root);
    // 左左情况
    if (balance > 1 && getBalance(root->left) >= 0)
        return rightRotate(root);
    // 左右情况
    if (balance > 1 && getBalance(root->left) < 0) {
        root->left = leftRotate(root->left);
        return rightRotate(root);
    }
    // 右右情况
    if (balance < -1 && getBalance(root->right) <= 0)
        return leftRotate(root);
    // 右左情况
    if (balance < -1 && getBalance(root->right) > 0) {
        root->right = rightRotate(root->right);
        return leftRotate(root);
    }

    return root;
}

       50
     /    \
   30      70
  /  \     / 
20    40  60
     /
   35

对于上面这种情况，删除 60，满足左右，我们先要对 30 进行左旋，然后对50进行右旋

          50
        /    \
      30       70
     /  \     /   \
   20    35  60     80
  /         /  \       \   
10        55   65      85
       /
     52

对于上面这种情况，删除 20，满足右左，我们先要对 70 进行右旋，然后对50进行左旋

7.2.3.4 中序遍历

// 中序遍历辅助函数
void inorderHelper(AVLNode<KeyType, ValueType>* node, std::vector<std::pair<KeyType, ValueType>>& res) const {
    if (node != nullptr) {
        inorderHelper(node->_left, res);
        res.emplace_back(node->_key, node->_value);
        inorderHelper(node->_right, res);
    }
}

能够将 key 从小到大依次遍历

7.2.4 AVLMap的操作

现在，我们将所有模板化的函数集成到一个模板类AVLMap中。这个类将提供如下功能：

put(const KeyType& key, const ValueType& value)：插入或更新键值对。
get(const KeyType& key)：查找键对应的值，返回指向值的指针，如果键不存在则返回nullptr。
remove(const KeyType& key)：删除指定键的键值对。
inorderTraversal()：中序遍历，返回有序的键值对列表。

// 插入或更新键值对
void put(const KeyType& key, const ValueType& value) {
    root = insertNode(root, key, value);
}

// 查找值，返回指向值的指针，如果键不存在则返回nullptr
ValueType* get(const KeyType& key) {
    return searchNode(root, key);
}

// 删除键值对
void remove(const KeyType& key) {
    root = deleteNode(root, key);
}

// 中序遍历，返回有序的键值对
std::vector<std::pair<KeyType, ValueType>> inorderTraversal() const {
    std::vector<std::pair<KeyType, ValueType>> res;
    inorderHelper(root, res);
    return res;
}

// 析构函数，释放所有节点的内存
~AVLMap() {
    // 使用后序遍历释放节点
    std::function<void(AVLNode<KeyType, ValueType>*)> destroy = [&](AVLNode<KeyType, ValueType>* node) {
        if (node != nullptr) {
            destroy(node->_left);
            destroy(node->_right);
            delete node;
        }
    };

    destroy(root);
}

7.2.5 完整代码

#pragma once
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <functional>

template <typename KeyType, typename ValueType>
struct AVLNode{
	KeyType _key;
	ValueType _value;
	int _height;
	AVLNode* _left, * _right;

	AVLNode(const KeyType& key, const ValueType& value)
		: _key(key), _value(value), _height(1), _left(nullptr), _right(nullptr) {}
};

template <typename KeyType, typename ValueType>
class AVLMap {
private:
	AVLNode<KeyType, ValueType>* root;

	int getHeight(AVLNode<KeyType, ValueType>* node) {
		if (node == nullptr) 
			return 0;
		return node->_height;
	}

	int getBalance(AVLNode<KeyType, ValueType>* node) {
		if (node == nullptr)
			return 0;
		return getHeight(node->_left) - getHeight(node->_right); // 左子树 - 右子树
	}

	AVLNode<KeyType, ValueType>* rightRotate(AVLNode<KeyType, ValueType>* y) {
		AVLNode<KeyType, ValueType>* x = y->_left;
		AVLNode<KeyType, ValueType>* T2 = x->_right;
		// 执行旋转
		x->_right = y;
		y->_left = T2;
		// 更新高度
		y->_height = std::max(getHeight(y->_left), getHeight(y->_right)) + 1;
		x->_height = std::max(getHeight(x->_left), getHeight(x->_right)) + 1;
		// 返回新的根
		return x;
	}

	AVLNode<KeyType, ValueType>* leftRotate(AVLNode<KeyType, ValueType>* x) {
		AVLNode<KeyType, ValueType>* y = x->_right;
		AVLNode<KeyType, ValueType>* T2 = y->_left;
		// 执行旋转
		y->_left = x;
		x->_right = T2;
		// 更新高度
		x->_height = std::max(getHeight(x->_right), getHeight(x->_left)) + 1;
		y->_height = std::max(getHeight(y->_right), getHeight(y->_left)) + 1;
		// 返回新的根
		return y;
	}

	AVLNode<KeyType, ValueType>* insertNode(AVLNode<KeyType, ValueType>* node, // 当前节点
		const KeyType& key, const ValueType& value) {
		// 执行BST的插入，递归调用
		if (node == nullptr) // 当执行到最后一层时，才会将节点插入至 nullptr 的位置
			return new AVLNode<KeyType, ValueType>(key, value);

		if (key < node->_key) // 如果插入的key值小于当前节点，那么插入当前节点的左子树
			node->_left = insertNode(node->_left, key, value);
		else if (key > node->_key) // 如果插入的key值小于当前节点，那么插入当前节点的左子树
			node->_right = insertNode(node->_right, key, value);
		else { // 如果插入key值等于当前节点key值，更新值
			node->_value = value;
			return node;
		}

		// 更新节点高度
		node->_height = std::max(getHeight(node->_left), getHeight(node->_right)) + 1;

		// 获取平衡因子
		int balance = getBalance(node);

		// 根据因子情况进行旋转
		// 左左情况
		if (balance > 1 && key < node->_left->_key)
			return rightRotate(node);

		// 右右情况
		if (balance < -1 && key > node->_right->_key)
			return leftRotate(node);

		// 左右情况
		if (balance > 1 && key > node->_left->_key) {
			node->_left = leftRotate(node->_left);
			return rightRotate(node);
		}

		// 右左情况
		if (balance < -1 && key < node->_right->_key) {
			node->_right = rightRotate(node->_right);
			return leftRotate(node);
		}

		return node;
	}

	AVLNode<KeyType, ValueType>* getMinValueNode(AVLNode<KeyType, ValueType>* node) {
		AVLNode<KeyType, ValueType>* cur = node;
		while (cur->_left != nullptr)
			cur = cur->_left;

		return cur;
	}

	ValueType* searchNode(AVLNode<KeyType, ValueType>* node, const KeyType& key) {
		if (node == nullptr)
			return nullptr;

		if (node->_key == key)
			return &(node->_value);
		else if (key < node->_key)
			return searchNode(node->_left, key);
		else
			return searchNode(node->_right,key);
	}

	AVLNode<KeyType, ValueType>* deleteNode(AVLNode<KeyType, ValueType>* root, const KeyType& key) {
		// 以 BST 方式删除
		if (root == nullptr)
			return root;

		if (key < root->_key)
			root->_left = deleteNode(root->_left, key);
		else if (key > root->_key)
			root->_right = deleteNode(root->_right, key);
		else { // 找到待删节点
			// 待删除节点无子树或只有一个子树
			if (root->_left == nullptr or root->_right == nullptr) {
				AVLNode<KeyType, ValueType>* temp = root->_left != nullptr ? root->_left : root->_right;
				// 若 temp 为空，说明待删除节点没有子节点
				if (temp == nullptr) {
					temp = root;
					root = nullptr; // 因为待删除节点没有子节点可以直接将待删除节点清空
				}
				else { // 待删除节点有一个子树
					*root = *temp; // 直接将待删除节点的子树复制到待删除节点的位置，相当于删除了待删除节点
				}

				delete temp;
			}
			else { // 待删除节点的左右子树都存在（难点）
				// 获取中序后继
				AVLNode<KeyType, ValueType>* temp = getMinValueNode(root->_right);
				// 保持待删除节点的左右子树不变，复制中序后继的键值对到此节点
				root->_key = temp->_key;
				root->_value = temp->_value;
				// 删除中序后继（同样会判断中序后继是否有左右子树）
				root->_right = deleteNode(root->_right, temp->_key);
			}
		}

		// 若节点删除完之后，整个树为空，则不需要旋转保持平衡
		if (root == nullptr)
			return root;

		// 更新高度
		root->_height = std::max(getHeight(root->_right), getHeight(root->_left)) + 1;
		// 获取平衡因子
		int balance = getBalance(root);
		// 左左情况
		if (balance > 1 && getBalance(root->_left) >= 0)
			return rightRotate(root);
		// 左右情况
		if (balance > 1 && getBalance(root->_left) < 0) {
			root->_left = leftRotate(root->_left);
			return rightRotate(root);
		}
		// 右右情况
		if (balance < -1 && getBalance(root->_right) <= 0)
			return leftRotate(root);
		// 右左情况
		if (balance < -1 && getBalance(root->_right) > 0) {
			root->_right = rightRotate(root->_right);
			return leftRotate(root);
		}

		return root;
	}

	// 中序遍历辅助函数
	void inorderHelper(AVLNode<KeyType, ValueType>* node, std::vector<std::pair<KeyType, ValueType>>& res) const {
		if (node != nullptr) {
			inorderHelper(node->_left, res);
			res.emplace_back(node->_key, node->_value);
			inorderHelper(node->_right, res);
		}
	}
	
public:
	AVLMap() :root(nullptr) {}

	// 插入或更新键值对
	void put(const KeyType& key, const ValueType& value) {
		root = insertNode(root, key, value);
	}

	// 查找值，返回指向值的指针，如果键不存在则返回nullptr
	ValueType* get(const KeyType& key) {
		return searchNode(root, key);
	}

	// 删除键值对
	void remove(const KeyType& key) {
		root = deleteNode(root, key);
	}

	// 中序遍历，返回有序的键值对
	std::vector<std::pair<KeyType, ValueType>> inorderTraversal() const {
		std::vector<std::pair<KeyType, ValueType>> res;
		inorderHelper(root, res);
		return res;
	}

	// 析构函数，释放所有节点的内存
	~AVLMap() {
		// 使用后序遍历释放节点
		std::function<void(AVLNode<KeyType, ValueType>*)> destroy = [&](AVLNode<KeyType, ValueType>* node) {
			if (node != nullptr) {
				destroy(node->_left);
				destroy(node->_right);
				delete node;
			}
		};

		destroy(root);
	}
};

该代码仍有很多地方需要优化改进：

内存管理：当前实现使用递归进行插入和删除，如果树非常深，可能会导致栈溢出。可以考虑使用迭代方法或优化递归深度。
缓存友好：使用自适应数据结构（如缓存友好的节点布局）可以提升性能。
多线程支持：当前实现不是线程安全的。如果需要在多线程环境中使用，需要添加适当的同步机制。

也可以添加其他功能：

迭代器：实现输入迭代器、中序遍历迭代器，以便支持范围基（range-based）for循环。
查找最小/最大键：提供方法findMin()和findMax()。
前驱/后继查找：在树中查找给定键的前驱和后继节点。
支持不同的平衡因子策略：例如，允许用户指定自定义的平衡策略。

8. 红黑树

8.1 基本概念

红黑树也是一种二叉搜索树（BST），因为AVL树在高度差大于1之后需要让它进行旋转处理来维持平衡状态，这个过程的成本不低，因此才开发出来了红黑树。

对于二叉搜索树（BST），如果插入的数据是随机的，那么它就是接近平衡的二叉树，平衡的二叉树，它的操作效率（查询，插入，删除）效率较高，时间复杂度是O（logN）。但是可能会出现一种极端的情况，那就是插入的数据是有序的（递增或者递减），那么所有的节点都会在根节点的右侧或左侧，此时，二叉搜索树就变为了一个链表，它的操作效率就降低了，时间复杂度为O(N)，所以可以认为二叉搜索树的时间复杂度介于O（logN）和O(N)之间。那么为了应对这种极端情况，红黑树就出现了，它是具备了某些特性的二叉搜索树，能解决非平衡树问题，红黑树是一种接近平衡的二叉树（说它是接近平衡因为它并没有像AVL树的平衡因子的概念，它只是靠着满足红黑节点的5条性质来维持一种接近平衡的结构，进而提升整体的性能，并没有严格的卡定某个平衡因子来维持绝对平衡）。其查找、插入、删除）的时间复杂度同样为 O(log n)。

红黑树在每个节点增加了一个存储位记录节点的颜色，可以是RED,也可以是BLACK；通过任意一条从根到叶子简单路径上颜色的约束，红黑树保证最长路径不超过最短路径的二倍，因而近似平衡（最短路径就是全黑节点，最长路径就是一个红节点一个黑节点，当从根节点到叶子节点的路径上黑色节点相同时，最长路径刚好是最短路径的两倍）。它同时满足以下五条特性：

节点颜色：每个节点要么是红色，要么是黑色。
根节点颜色：根节点是黑色。
叶子节点颜色：所有叶子节点（NULL 节点，即空节点）都是黑色的。这里的叶子节点不存储实际数据，仅作为树的终端。
红色节点限制：如果一个节点是红色的，则它的两个子节点都是黑色的。也就是说，红色节点不能有红色的子节点（不能有2个连续的红色节点，但可以有2个连续的黑色节点）。
黑色平衡：从任意节点到其所有后代叶子节点的路径上，包含相同数量的黑色节点。这被称为每条路径上的黑色高度相同。

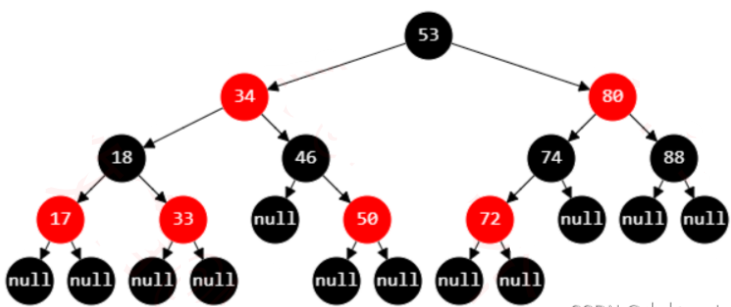
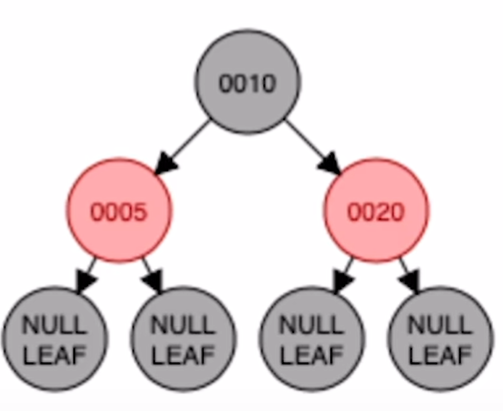
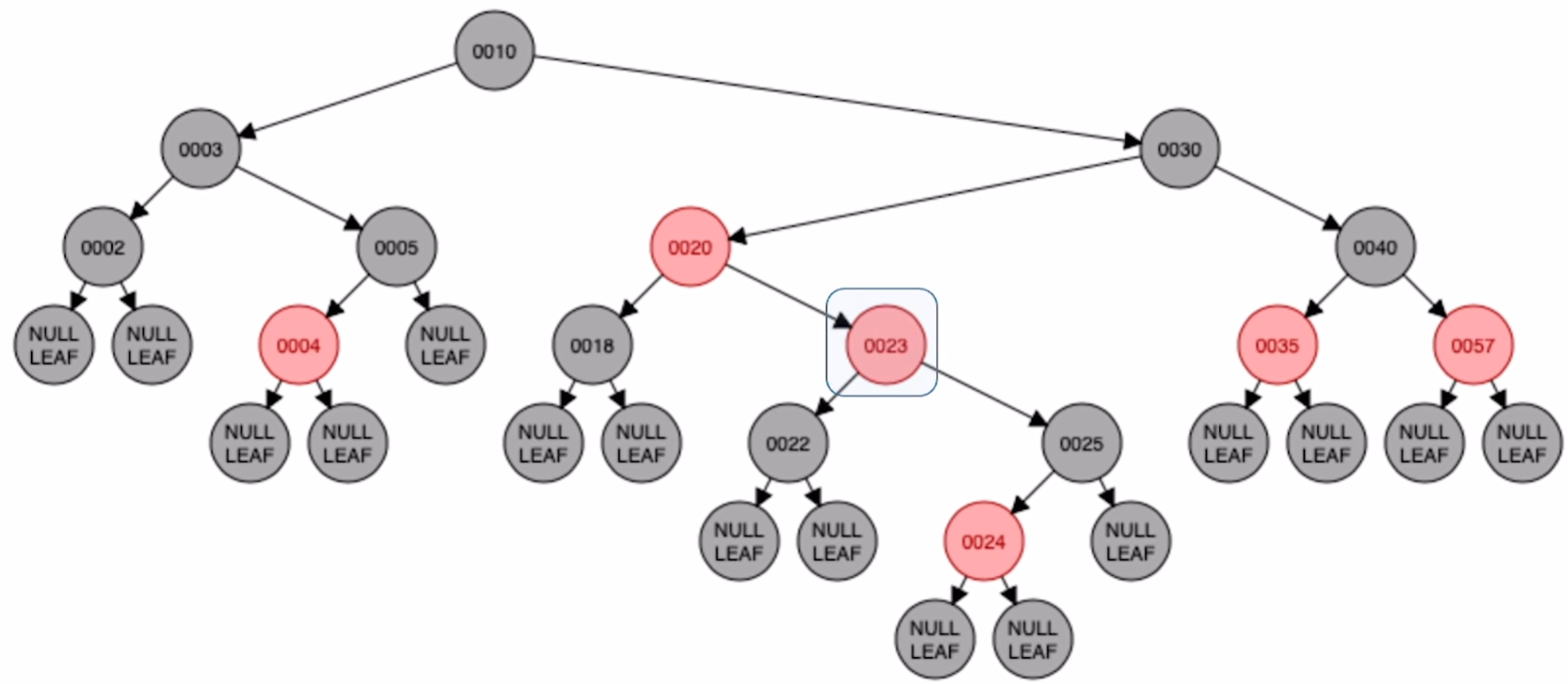
判断下面的树是否为红黑树：

上面这棵树首先很容易就能知道是满足性质1-4条的，关键在于第5条性质，可能乍一看好像也是符合第5条的，但实际就会陷入一个误区，直接将图上的最后一层的节点看作叶子节点，这样看的话每一条从根节点到叶子节点的路径确实都经过了3个黑节点。

但实际上，在红黑树中真正被定义为叶子节点的，是那些空节点，如下图。

这样一来，路径1有4个黑色节点（算上空节点），路径2只有3个黑色节点，这样性质5就不满足了，所以这棵树并不是一个红黑树节点。

红黑树 vs AVL 树

特性	红黑树 (Red-Black Tree)	AVL 树 (AVL Tree)
平衡性	相对不严格，每个路径上的黑色节点相同。	更严格，任意节点的左右子树高度差不超过1。
插入/删除效率	较快，插入和删除操作较少的旋转，适用于频繁修改的场景。	较慢，插入和删除可能需要多次旋转，适用于查找操作多于修改的场景。
查找效率	O(log n)	O(log n)，常数因子更小，查找速度略快。
实现复杂度	相对简单，旋转操作较少。	实现较复杂，需严格维护高度平衡。
应用场景	操作频繁、需要快速插入和删除的场景。	查找操作频繁、插入和删除相对较少的场景。

之所以红黑树的查找效率低于AVL树是因为，红黑树在查找时和普通的相对平衡的二叉搜索树（BST）的效率相同，都是通过相同的方式来查找的，没有用到红黑树特有的特性。但如果插入的时候是有序数据，那么红黑树的查询效率就比二叉搜索树（BST）要高了，因为此时二叉搜索树不是平衡树，它的时间复杂度O(N)。

红黑树不是严格意义上的高度平衡树，其树高可能相对 AVL 树略高，所以查找操作的平均时间复杂度虽然也是O(logn)，但在相同节点数量的情况下，查找路径可能会略长一些，查找效率相对 AVL 树稍低。而AVL树严格的平衡特性保证了 AVL 树的查找路径长度相对较短，查找操作的性能更稳定，在查找密集型的应用场景中，AVL 树通常能够更快地找到目标节点，具有更好的查找性能。

常数因子差异：

红黑树的每次比较需要处理颜色标志（虽然硬件层面影响微小，但累积效应存在）。
红黑树的路径长度方差更大（部分路径较长），可能导致更多的分支预测失败（CPU 流水线效率降低）。

8.2 基本操作

8.2.1 插入

8.2.1.1 概念

红黑树的插入操作通常分为以下两个主要步骤：

标准二叉搜索树插入：根据键值比较，将新节点插入到合适的位置，初始颜色为红色（染成红色是为了保证第5条性质）。
插入后的修正（Insert Fixup）：通过重新着色和旋转操作，恢复红黑树的五大性质。

BST 的插入不过多介绍，保证左子树节点值<根节点值<右子树节点值即可，这里详细分析插入后的修正。

因为新插入的节点 z 默认颜色是红色，则需满足以下情况：

父节点为黑色：
- 如果 z 的父节点是黑色的，那么插入操作不会破坏红黑树的性质，修正过程结束。
父节点为红色：
- 情况1：z 的叔叔节点（即 z 的父节点的兄弟节点）也是红色。
  - 将父节点和叔叔节点重新着色为黑色。
  - 将祖父节点重新着色为红色。
  - 将 z 指向祖父节点，继续检查上层节点，防止高层的性质被破坏。
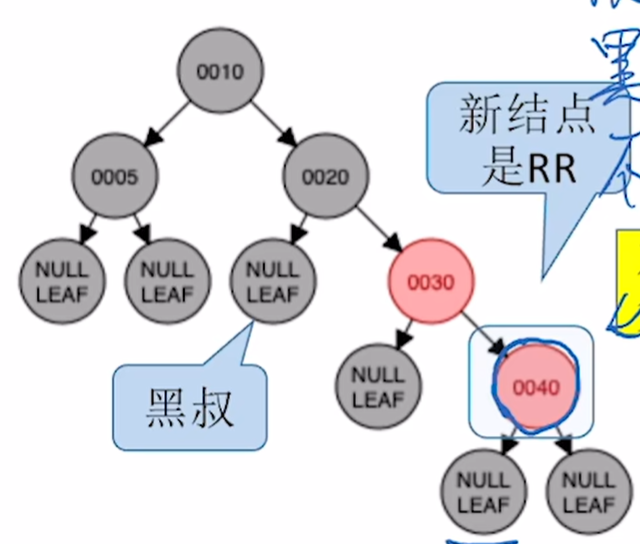
- 情况2：z 的叔叔节点是黑色
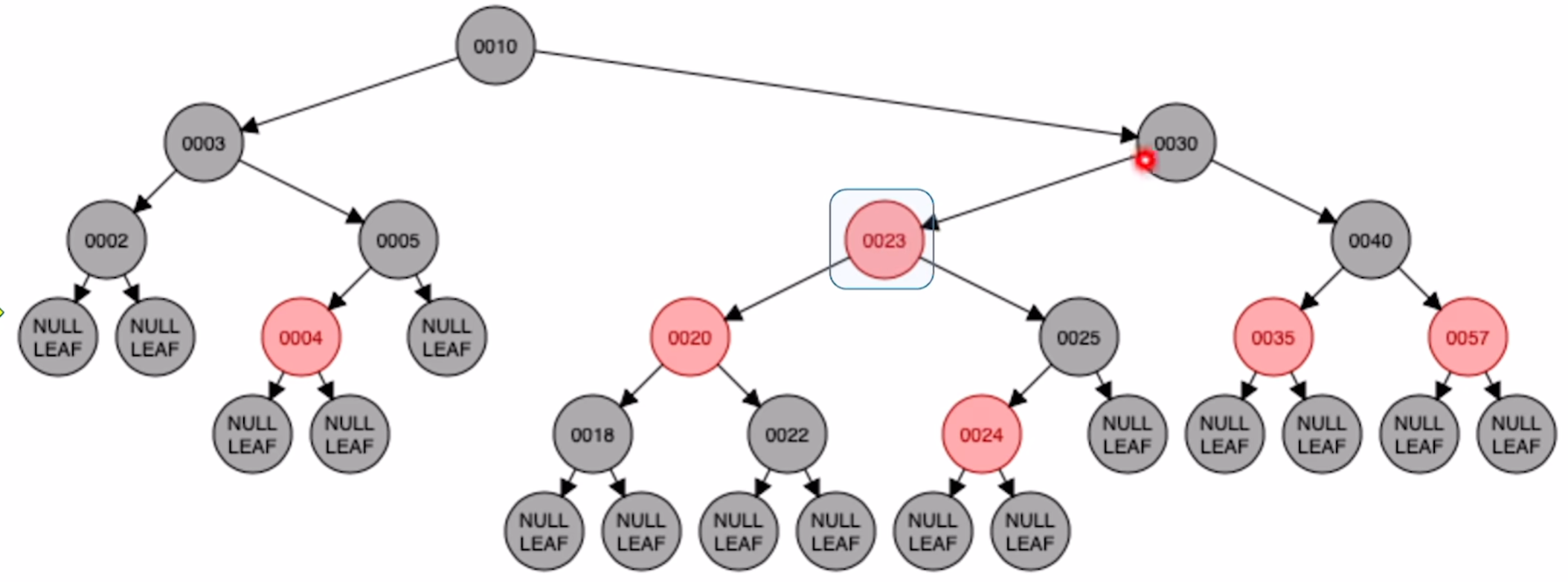
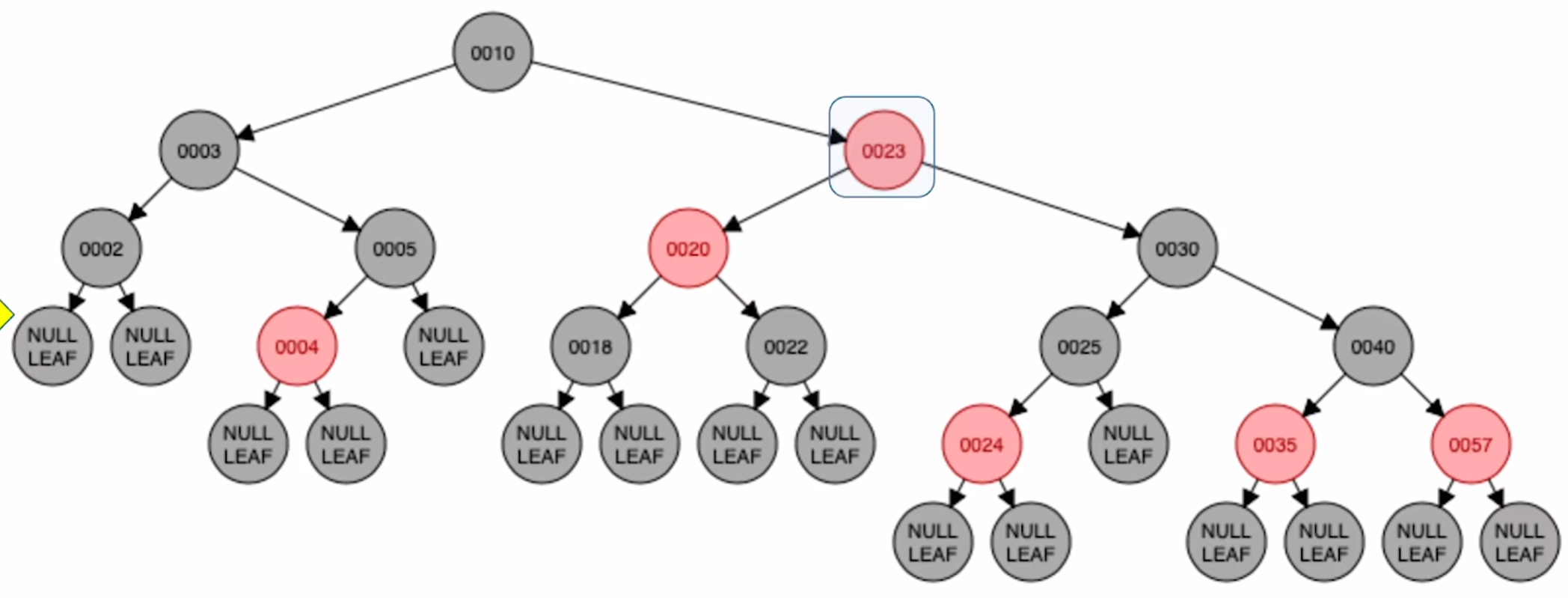
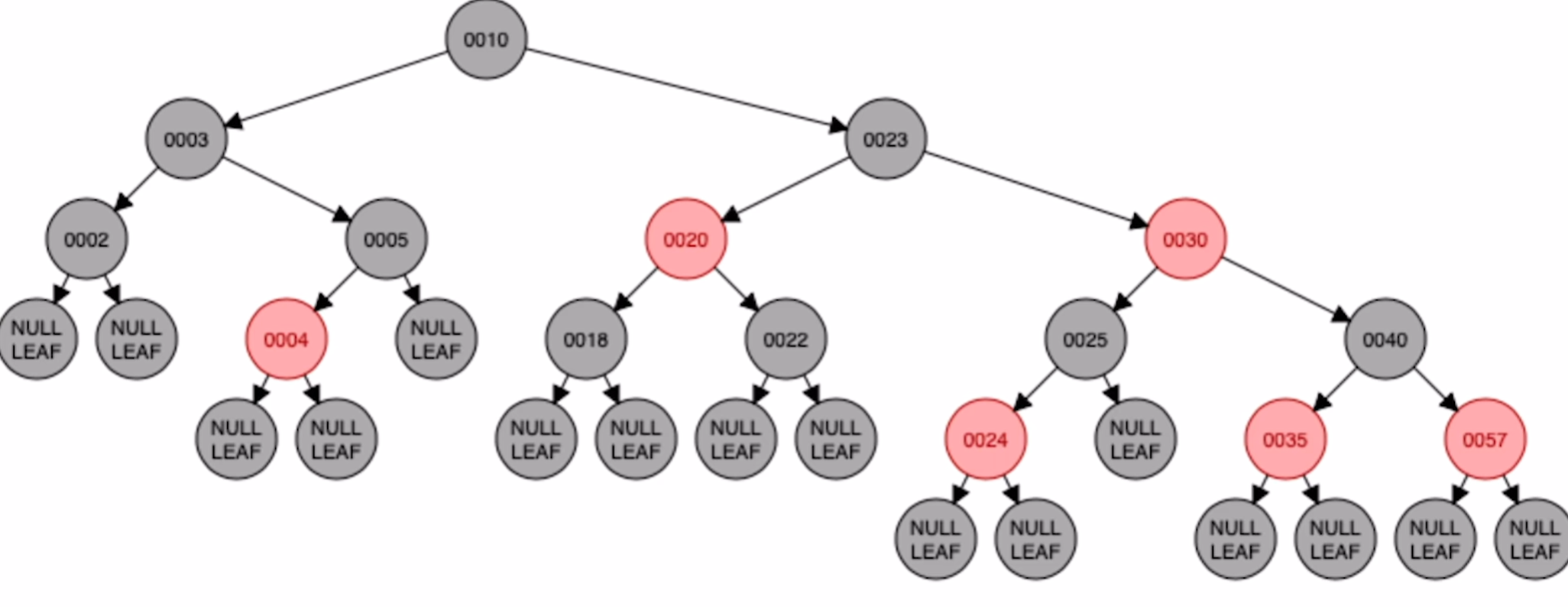
  - LL型：右单旋，父换爷+染色
  - RR型：左单旋，父换爷+染色
  - LR型：左、右双旋，儿换爷+染色
  - RL型：右、左双旋，儿换爷+染色

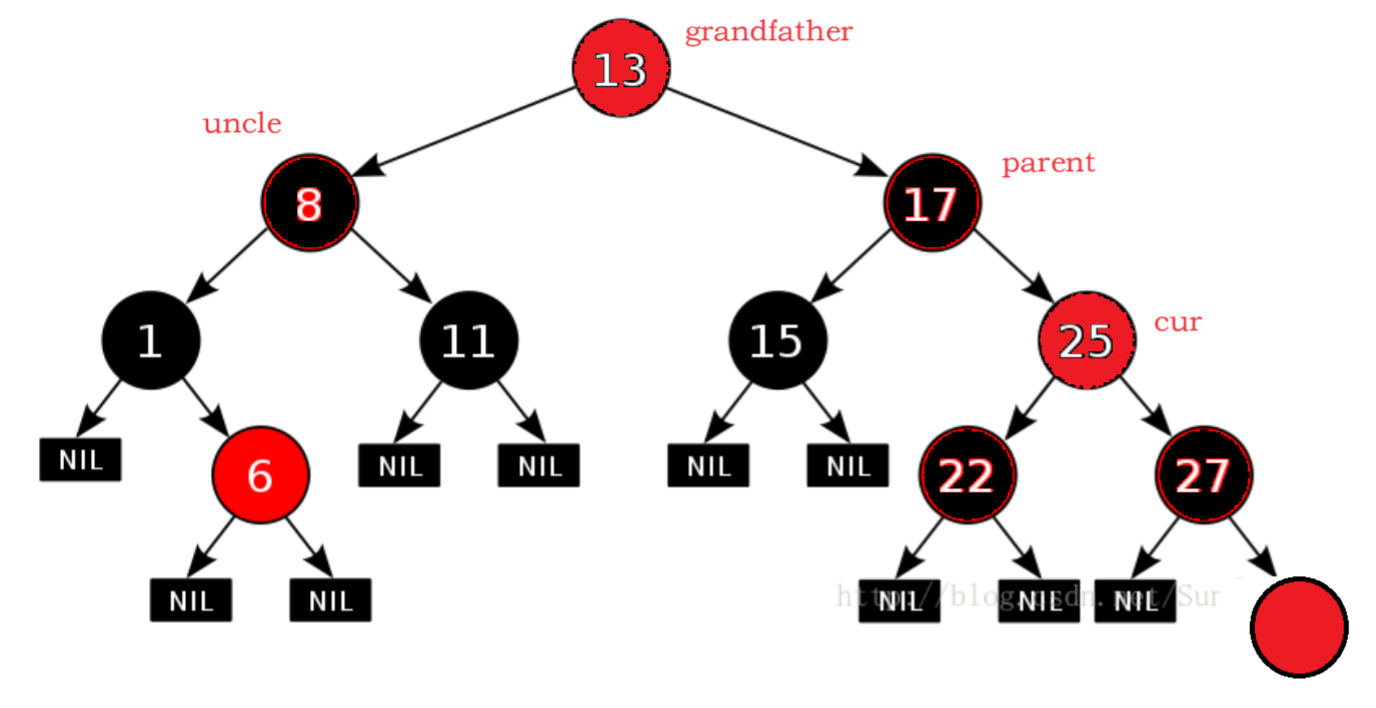
针对情况一：

在这里插入图片描述

将父节点和叔叔节点重新着色为黑色，将祖父节点重新着色为红色

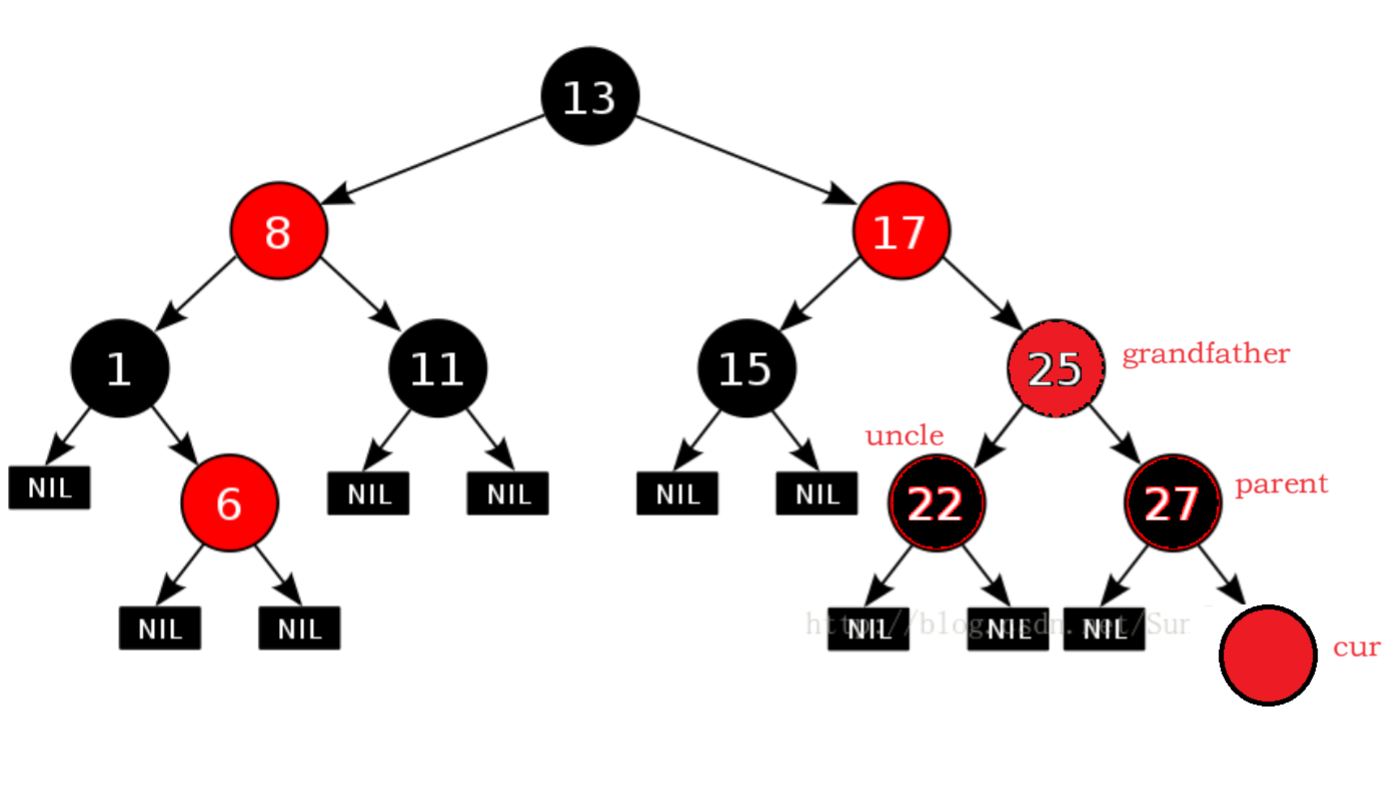
在这里插入图片描述

将 z 指向祖父节点（将grandfather看作插入节点，修正上层颜色，而不是将插入节点覆盖到grandfather），继续检查上层节点，防止高层的性质被破坏。

在这里插入图片描述

将父节点和叔叔节点重新着色为黑色，将祖父节点重新着色为红色。此时祖父节点是根节点，则将祖父节点改为黑色。

针对情况二：

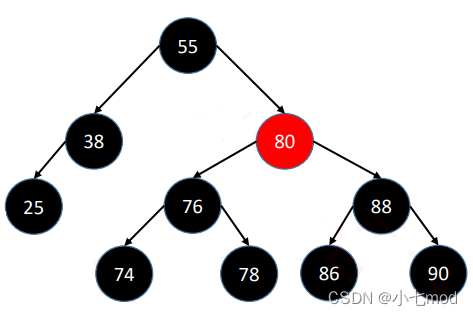
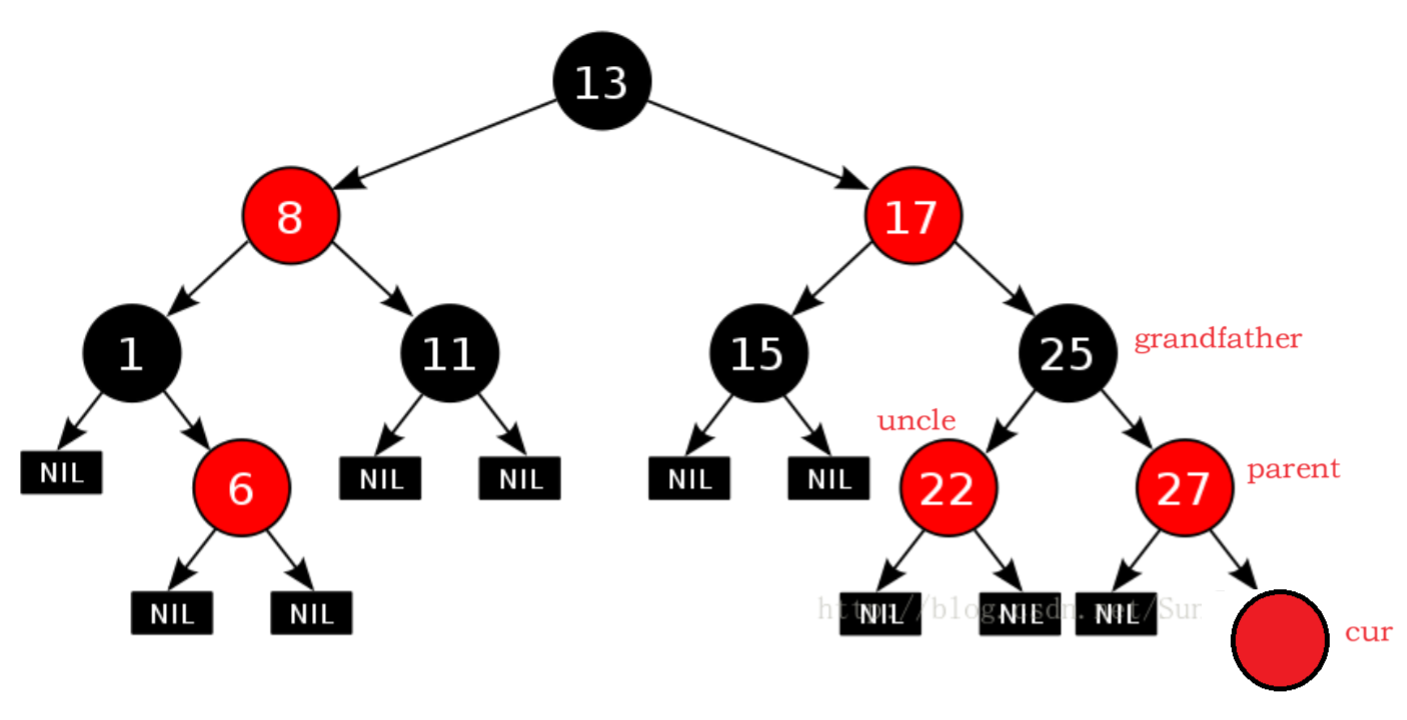
a）LL型别：插入 5

对祖父进行右旋

将父节点重新着色为黑色，祖父染色为红色

b）RR型：插入 40

对祖父左单旋

将祖父节点染红，父亲节点染黑

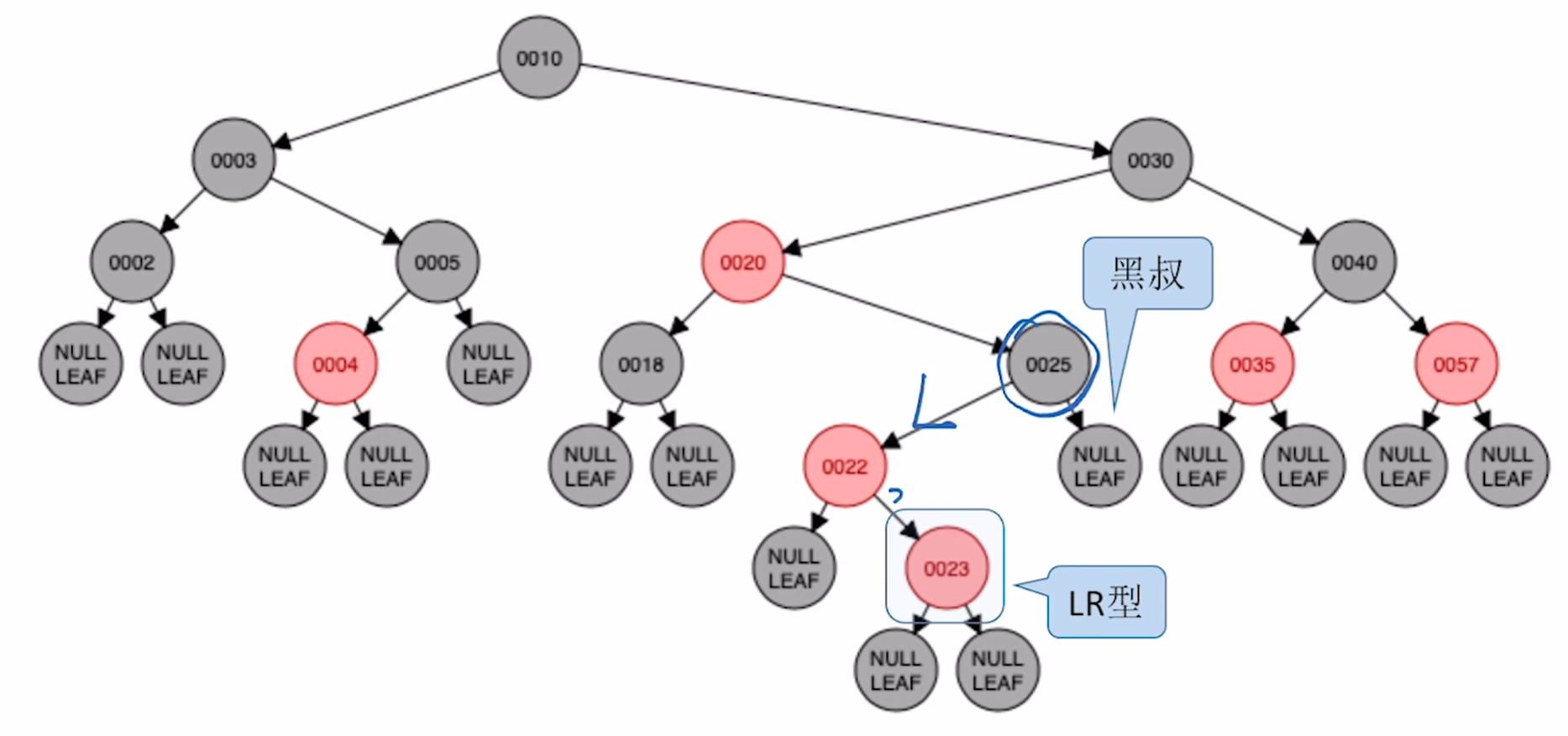
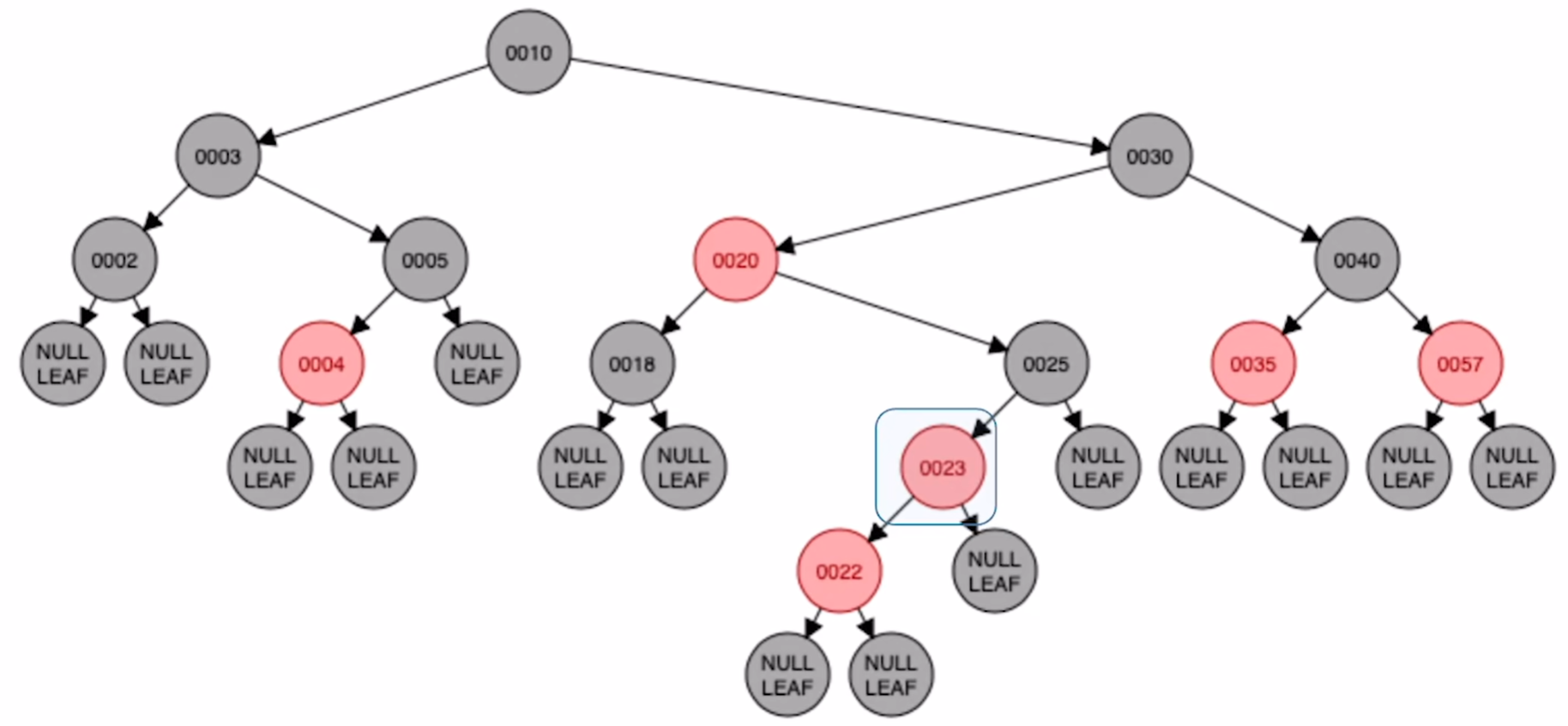
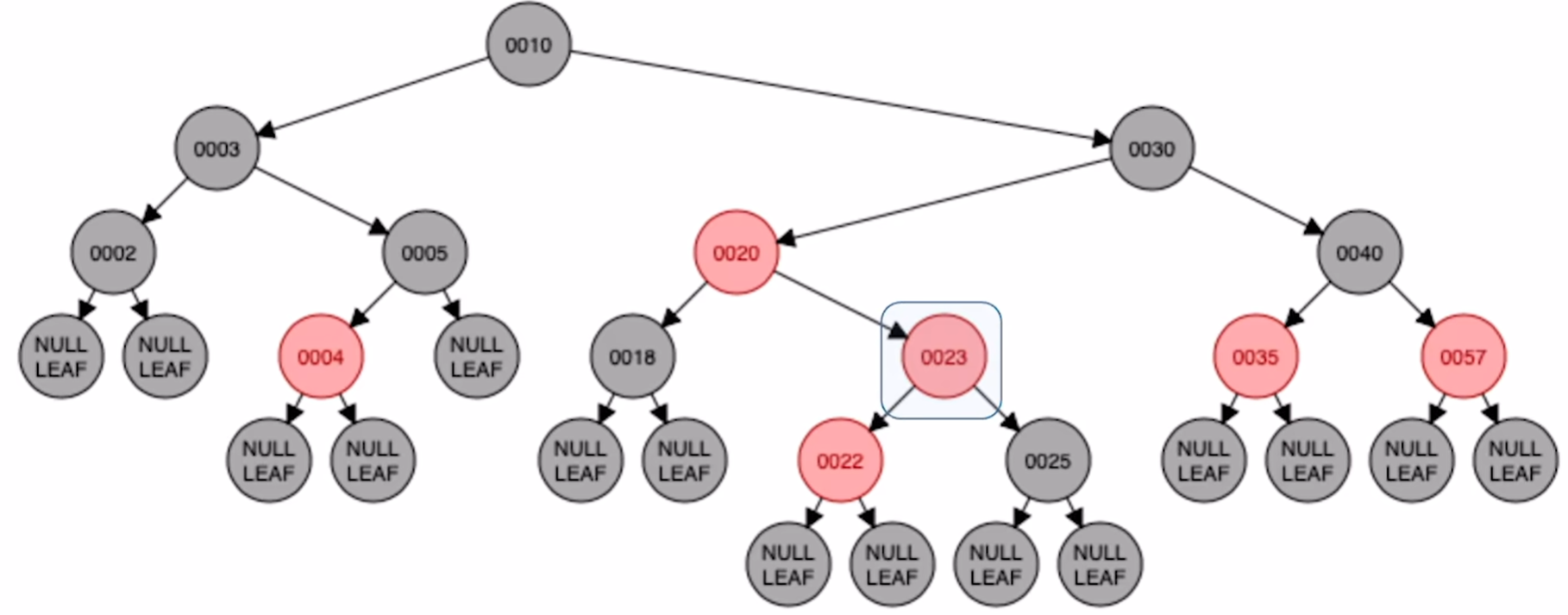
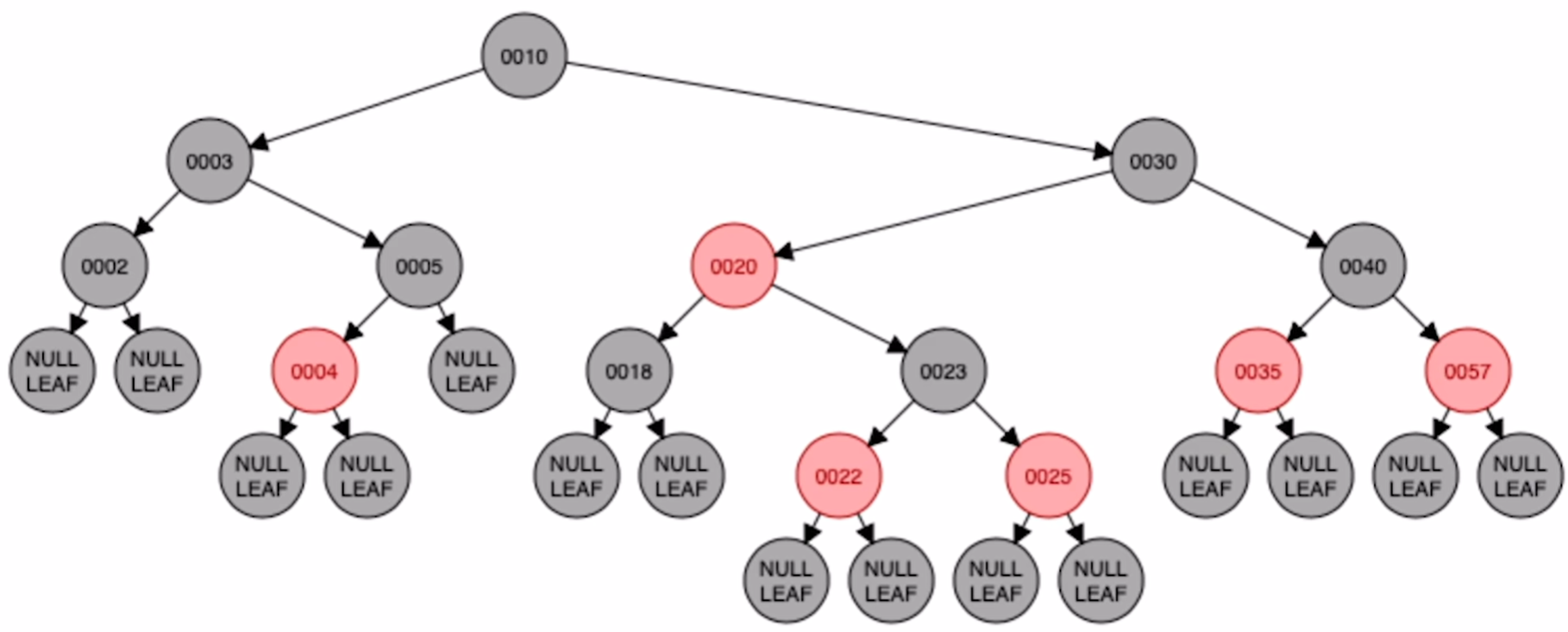
c）LR型：插入 23

对父节点进行左旋

对 25 进行右旋

将原本的祖父节点和插入节点颜色互换

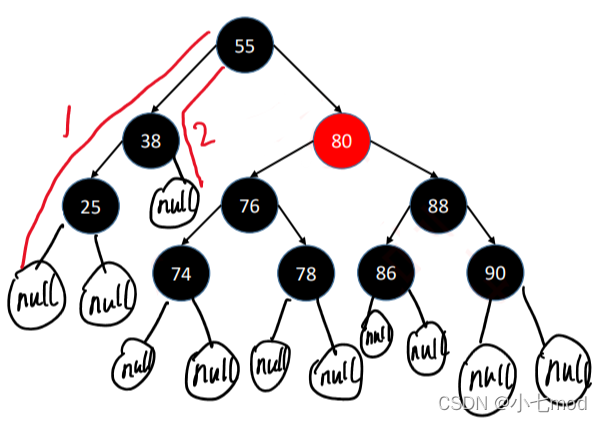
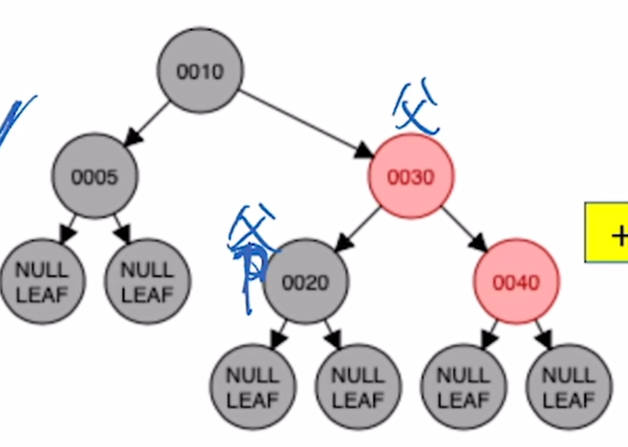
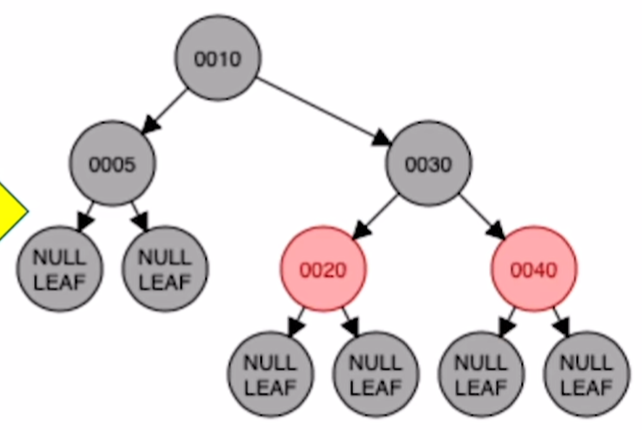
d）RL型别：情况一处理完转到祖父节点后发现，23 是RL型别

对20进行右旋

对30进行左旋

30和23颜色互换

8.2.1.2 代码

bool Insert(const pair<K,V> &kv)
{
  //1. 按照二叉搜索的树规则插入新节点
  Node* &root = GetRoot(); //这里注意要用引用接收返回值
  if(root == nullptr)
  {
  	//如果新插入的节点是根节点，需要将节点变为黑色以满足性质2
    root = new Node(kv, BLACK); //因为GetRoot返回指针的引用，所以改的实际是_phead->_parent
    root->_parent = _phead;
    _phead->_left = root;
    _phead->_right = root;
    return true;
  }

  Node *cur = root;
  Node *parent = nullptr;
  while(cur != nullptr)
  {
    if(kv.first > cur->_kv.first)
    {
      parent = cur;
      cur = cur->_right;
    }
    else if(kv.first < cur->_kv.first)
    {
      parent  = cur;
      cur = cur->_left;
    }
    else{
      return false;
    }
  }
  
  cur = new Node(kv,RED); //新插入的节点默认是红色的
  if(kv.first > parent->_kv.first)
  {
    parent->_right = cur;
  }
  else{
    parent->_left = cur;
  }
  cur->_parent = parent;
 
  //2.检测新节点插入后，红黑树的性质是否造到破坏。
  //如果父节点是黑色的，没有违反红黑树的任何性质，则不需要调整；
  //但如果父节点颜色为红色时，就违反了性质3：路径上不能有两个连续的红色结点。
  //上一次循环中grandparent 为根节点，此次循环parent == _phead
  while(parent != _phead && parent->_color == RED) 
  {
    Node *grandparent = parent->_parent;
    //断言检查：grandparent一定不为空且为黑色！
    assert(grandparent != nullptr);
    assert(grandparent->_color == BLACK);

    Node *uncle = grandparent->_left;
    if(parent == grandparent->_left)
      uncle = grandparent->_right;

    if(uncle != nullptr && uncle->_color == RED) //情况一：uncle存在且为红
    {
      parent->_color = uncle->_color = BLACK; //变色
      grandparent->_color = RED;
      cur = grandparent; //继续向上调整
      parent = cur->_parent;
    }
    else //情况二、三：uncle不存在或uncle存在且为黑
    {
      if(parent == grandparent->_left)
      {
        if(cur == parent->_left) //左左
        {
          RotateR(grandparent); //右单旋
          parent->_color = BLACK; //变色
          grandparent->_color = RED;
        }
        else{ //左右
          RotateL(parent); //左右双旋
          RotateR(grandparent);
          cur->_color = BLACK; //变色
          grandparent->_color = RED;
        }
      }
      else{
        if(cur == parent->_right) //右右
        {
          RotateL(grandparent); //左单旋
          parent->_color = BLACK; //变色
          grandparent->_color = RED;
        }
        else{ //右左
          RotateR(parent); //右左双旋
          RotateL(grandparent);
          cur->_color = BLACK; //变色
          grandparent->_color = RED;
        }
      }
      //旋转变色后无需继续调整，直接退出循环。
      break; 
    } //end of else
  } //end of while
  
  //如果在调整过程中将根节点变为红色，记得重新变回黑色。
  if(parent == _phead) 
    root->_color = BLACK;
  //令头节点的左指针指向红黑树的最左节点
  _phead->_left = LeftMost();
  //令头节点的右指针指向红黑树的最右节点
  _phead->_right = RightMost();
  return true;
}

8.2.2 删除

删除操作同样重要且复杂，因为它可能破坏红黑树的多个性质。与插入类似，删除操作也需要两个主要步骤：

标准二叉搜索树删除：按照 BST 的规则删除节点。
删除后的修正（Delete Fixup）：通过重新着色和旋转操作，恢复红黑树的性质。

删除操作分为以下步骤：

定位要删除的节点：
- 如果要删除的节点 z 有两个子节点，则找到其中序后继节点 y（即 z 的右子树中的最小节点）。
- 将 y 的值复制到 z，然后将删除目标转移到 y。
删除节点：
- 若 y 只有一个子节点 x（可能为 NIL），则用 x 替代 y 的位置。
- 记录被删除节点的原颜色 y_original_color。
删除修正（仅当 y_original_color 为黑色时）：
- 因为删除一个黑色节点会影响路径上的黑色数量，需通过多次调整来恢复红黑树的性质。

修正流程：

初始化：设 x 为替代被删除的节点的位置，x 可能为实际节点或 NIL 节点。
循环修正：
- 当 x 不是根节点，且 x 的颜色为黑色，进入修正循环。
- 判断 x 是其父节点的左子节点还是右子节点，并相应地设定兄弟节点 w。
处理不同情况：

情况1：w 是红色的。

情况2：w 是黑色，且 w 的两个子节点都是黑色。

情况3：w 是黑色，且 w 的左子节点是红色，右子节点是黑色。

情况4：w 是黑色，且 w 的右子节点是红色。

将 w 重新着色为黑色。
将 x 的父节点重新着色为红色。
对 x 的父节点进行左旋转或右旋转，取决于是左子节点还是右子节点。
更新 w，继续修正过程。
将 w 重新着色为红色。
将 x 设为其父节点，继续修正。
将 w 的左子节点重新着色为黑色。
将 w 重新着色为红色。
对 w 进行右旋转或左旋转，取决于是左子节点还是右子节点。
更新 w，进入情况4。
将 w 的颜色设为 x 的父节点颜色。
将 x 的父节点重新着色为黑色。
将 w 的右子节点重新着色为黑色。
对 x 的父节点进行左旋转或右旋转，取决于是左子节点还是右子节点。
结束修正。

最终步骤：将 x 设为根节点，并将其颜色设为黑色，确保根节点的颜色为黑色。

8.3 红黑树节点

enum Color { RED, BLACK };

template <typename Key, typename Value>
struct RBTreeNode {
    Key _key;
    Value _value;
    Color _color;
    RBTreeNode* _parent;
    RBTreeNode* _left;
    RBTreeNode* _right;

    RBTreeNode(Key k, Value v)
        : _key(k), _value(v), _color(RED), _parent(nullptr), _left(nullptr), _right(nullptr) {}
};

9. unordered_map

9.1 哈希表概念

哈希表（散列表）是一种基于键值对的数据结构，通过哈希函数（Hash Function）将键映射到表中的一个索引位置，以实现快速的数据访问。哈希表的关键特性包括：

哈希函数：将键映射到表中一个特定的桶（Bucket）或槽（Slot）。
同义词：若不同的关键字通过哈希函数映射到同一个值，则为同义词
冲突解决：当不同的键通过哈希函数映射到同一个桶时，需要一种机制来处理这些冲突。常见的方法有拉链法（Separate Chaining）和开放定址法（Open Addressing）。
装填因子：表中已存储元素的数量与表长度之间的比率。

1）哈希表的作用
哈希表就是在关键字和存储位置之间建立对应关系，使得元素的查找可以以**O(1)**的效率进行，其中关键字和存储位置之间是通过散列函数建立关系，记为：
$$
Loc(i)=Hash(key)
$$
2）常见的哈希函数

a. 除留余数法——H(key)=key%p

哈希表表长为m，取一个不大于m但最接近或等于m的质数p（除了1和本身外，不能被其他自然数整除的数）

b. 直接定址法——H(key)=key or H(key)=a*key + b

3）冲突解决方法

a. 拉链法

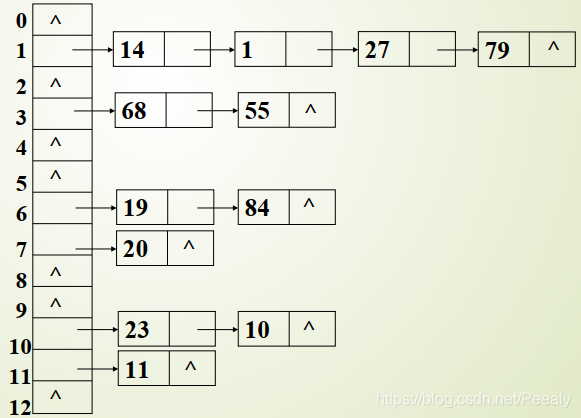
将具有相同存储地址的关键字链成一单链表，m个存储地址就设m个单链表，然后用一个数组将m个单链表的表头指针存储起来，形成一个动态的结构，假设散列函数为 Hash(key) = key %13，其拉链存储结构为:

在这里插入图片描述

b. 开放定址法

可存放新表项的空闲地址既向它的同义词表项开放，又向它的非同义词表项开放，m 是表长：
$$ {$H_i=(H(key)+d_i)%m$}
H_i=(H(key)+d_i)%m
$$
主要有以下三种处理方式：

① 线性探测法：d_i = 1,2,3,…,m-1; 即发生冲突时（d_i：第i次冲突），每次往后探测相邻的下一个单元是否为空。该方法可能会导致冲突处理函数值域大于本来的值域，但无妨。

例如，有一组关键字(14,36,42,38,40,15,19,12,51,65,34,25)，若表长 m 为15，散列函数为hash(key)=key%13，则可采用线性探测法处理冲突，构造该散列表。

按照关键字顺序，根据散列函数计算散列地址，如果该地址空间为空，则直接放入；如果该地址空间已存储数据，则采用线性探测法处理冲突。

[1] hash(14)=14%13=1，将14放入1号空间（下标为1）；hash(36)=36%13=10，将36放入10号空间；hash(42)=42%13=3，将42放入3号空间；hash(38)=38%13=12，将38放入12号空间。

在这里插入图片描述

[2] hash(40)=40%13=1，1号空间已存储数据，采用线性探测法处理冲突。

hash′(40)=(hash(40)+di )%m ，di =1,…,m -1

d1 =1：hash′(40)=(1+1)%15=2，2号空间为空，将40放入2号空间，即hash(40)=40%13=1→2。

在这里插入图片描述

[3] hash(15)=15%13=2，2号空间已存储数据，发生冲突，采用线性探测法处理冲突。

hash′(15)=(hash(15)+di )%m ，di =1,…,m -1

d1 =1：hash′(15)=(2+1)%15=3，3号空间已存储数据，继续进行线性探测。
d2 =2：hash′(15)=(2+2)%15=4，4号空间为空，将15放入4号空间。
即hash(15)=15%13=2→3→4。

在这里插入图片描述

[4] hash(19)=19%13=6，将19放入6号空间；hash(12)=12%13=12，12号空间已存储数据，采用线性探测法处理冲突。

hash′(12)=(hash(12)+di )%m ，di =1,…,m -1

d 1 =1：hash′(12)=(12+1)%15=13，12号空间为空，将12放入13号空间，即hash(12)=12%13=12→13。

在这里插入图片描述

[5] hash(51)=51%13=12，12号空间已存储数据，采用线性探测法处理冲突。

hash′(51)=(hash(51)+di )%m，di =1,…,m -1

d1 =1：hash′(51)=(12+1)%15=13，13号空间已存储数据，继续进行线性探测。
d2 =2：hash′(51)=(12+2)%15=14，14号空间为空，将51放入14号空间。
即hash(51)=51%13=12→13→14。

在这里插入图片描述

[6] hash(65)=65%13=0，将65放入0号空间；hash(34)=34%13=8，将34放入8号空间；

hash(25)=12%13=12，12号空间已存储数据，采用线性探测法处理冲突。

hash′(25)=(hash(25)+di )%m ，di =1,…,m -1

d1 =1：hash′(25)=(12+1)%15=13，13号空间已存储数据，继续进行线性探测。
d2 =2：hash′(25)=(12+2)%15=14，14号空间已存储数据，继续进行线性探测。
d3 =3：hash′(25)=(12+3)%15=0，0号空间已存储数据，继续进行线性探测。
d4 =4：hash′(25)=(12+4)%15=1，1号空间已存储数据，继续进行线性探测。
d5 =5：hash′(25)=(12+5)%15=2，2号空间已存储数据，继续进行线性探测。
d6 =6：hash′(25)=(12+6)%15=3，3号空间已存储数据，继续进行线性探测。
d7 =7：hash′(25)=(12+7)%15=4，4号空间已存储数据，继续进行线性探测。
d8 =8：hash′(25)=(12+8)%15=5，5号空间为空，将25放入5号空间
即hash(25)=25%13=12→13→14→0→1→2→3→4→5。

在这里插入图片描述

注意：线性探测法很简单，只要有空间，就一定能够探测到位置。但是，在处理冲突的过程中，会出现非同义词之间对同一个散列地址发生争夺的现象，称之为“堆积”。例如，上图中25和38是同义词，25和12、51、65、14、40、42、15均非同义词，却探测了9次才找到合适的位置，大大降低了查找效率。

②平方探测法：不同于前面线性探测法依次顺序查看下一个位置是否能存储元素，平方探测的规则是以 d_i = 1^2, -1^2, 2^2, -2^2,…, k^2, -k^2，其中 k <= m / 2。

当 ( H(key) + d_i ) < 0 或 > m 时，从表尾或表头重新开始。

使用平方探测法时，哈希表表长 m 必须是一个 4j + 3 的素数，才能探测到所有位置。

例】设关键词序列为{47,7,29,11,9,84,54,20,30}，散列表表长TableSize = 11，散列函数为：key % 11，用平方探测法处理冲突，列出依次插入后的散列表


操作 / 地址	0	1	2	3	4	5	6	7	8	9	10	说明
插入 47				47								无冲突
插入 7				47				7				无冲突
插入 29				47				7	29			d_i = 1
插入 11	11			47				7	29			无冲突
插入 9	11			47				7	29	9		无冲突
插入 84	11			47			84	7	29	9		d_2 = -1
插入 54	11			47			84	7	29	9	54	无冲突
插入 20	11		20	47			84	7	29	9	54	d_3 = 4
插入 30	11	30	20	47			84	7	29	9	54	d_3 = 4

③伪随机序列法：d_i 是一个伪随机序列

2025-04-30 12:24:32 # 面试 #C++容器

1. String类

1.1 初始化

1.2 字符串操作

1.2.1 拼接

1.2.2 清空、删除

1.2.3 比较字符串

1.2.4 修改字符串

1.2.5 字符串查询

1.2.6 判断字符串中的字符字母/数字/大小写

1.3 其他高级用法

1.3.1 字符串流（stringstream）

1.3.2 正则表达式与字符串匹配

1.4 简单的例子

示例项目1：简易文本分析器

示例项目2：用户输入验证工具

2. Vector

2.1 初始化

2.2 vector容器操作

2.2.1 vector的大小和容量

2.2.2 添加和删除

2.2.3 访问

2.2.4 遍历

2.2.5 vector修改

2.3 常用算法

2.3.1 排序

2.3.2 反转reverse()

2.3.3 查找find()

3. list

3.1 初始化

3.2 list操作

3.2.1 list的大小和容量

3.2.2 访问

3.2.3 常见修改操作

3.2.4 常见操作函数

4. deque

4.1 初始化

4.2 成员函数

5. 三种序列式容器的特点

6. map、unordered_map

6.1 map 初始化

6.2 map 成员方法

6.3 unordered_map 初始化

6.4 unordered_map 成员方法

7. AVL实现map

7.1 基本概念

7.2 实现

7.2.1 模板化AVL树节点

7.2.2 辅助函数模板化

7.2.2.1 获取节点高度

7.2.2.2 获取平衡因子

7.2.2.3 右旋

7.2.2.4 左旋

7.2.3 AVL树的核心操作模板化

7.2.3.1 节点插入

7.2.3.2 获取最小值节点

7.2.3.3 查找给定节点的value值

7.2.3.3 删除节点（BST节点删除方式）

7.2.3.4 中序遍历

7.2.4 AVLMap的操作

7.2.5 完整代码

8. 红黑树

8.1 基本概念

8.2 基本操作

8.2.1 插入

8.2.1.1 概念

8.2.1.2 代码

8.2.2 删除

8.3 红黑树节点

9. unordered_map

9.1 哈希表概念

1.3.1 字符串流（`stringstream`）