1. 毒药问题
给你1000瓶水,只有一瓶有毒,给你无限的老鼠,可以让每只老鼠喝任意瓶(可以是多瓶)的水,毒药会在24小时后发作,请问在一天用最少的老鼠找出哪一瓶有毒?
解法1:
利用二进制位的唯一性,将 1000 瓶水编号为0~999(共 1000 个编号),每个编号转换为10 位二进制数(因为 2^10=1024≥1000)。每只老鼠对应一个二进制位:
- 第 i 只老鼠喝所有编号中第 i 位为 1的瓶子。
- 24 小时后,根据死亡老鼠的位置(二进制位为 1)组合出毒瓶的编号。
具体步骤:
- 编号转换:将每瓶水的编号(0~999)转换为 10 位二进制数(不足补前导零)。
例:5→0000000101(第 1、3 位为 1)。 - 老鼠分配:
- 第 0 只老鼠:喝所有第 0 位为 1的瓶子(共 500 瓶,如 1,3,5,…)。
- 第 1 只老鼠:喝所有第 1 位为 1的瓶子(如 2,3,6,7,…)。
- …
- 第 9 只老鼠:喝所有第 9 位为 1的瓶子(如 512~1023,共 512 瓶)。
- 结果解码:
- 若第 0、2、4 只老鼠死亡,对应二进制位
10101(假设其他位为 0),转换为十进制即21,则第 21 瓶有毒。
- 若第 0、2、4 只老鼠死亡,对应二进制位
解法2:
- 将 1000 瓶水映射到三维空间
(x, y, z),其中 x,y,z∈[0,9](共 10×10×10=1000 个坐标)。 - 每组 10 只老鼠:
- X 组(10 只):第 i 只喝所有 x=i 的瓶子(100 瓶 / 只)。
- Y 组(10 只):第 j 只喝所有 y=j 的瓶子。
- Z 组(10 只):第 k 只喝所有 z=k 的瓶子。
- 结果解码:若 X 组第 a 只、Y 组第 b 只、Z 组第 c 只死亡,则毒瓶坐标为
(a, b, c)。
2. 分金条问题
问题: 你让工人为你工作7天,回报是一根金条,这个金条平分成相连的7段,你必须在每天结束的时候给他们一段金条。如果只允许你两次把金条弄断,你如何给你的工人付费?
解答:切两刀,分为1/7、2/7、4/7三段。
第一天给 1/7;
第二天给 2/7,要回 1/7;
第三天给 1/7 ;
第四天给 4/7 要回 1/7 + 2/7;
第五天给 1/7;
第六天给 2/7,要回 1/7;
第七天给 1/7
3. 飞鸟问题
问题:有一辆火车以每小时 15 公里的速度离开北京直奔广州,同时另一辆火车每小时 20 公里的速度从广州开往北京。如果有一只鸟,以 30 公里每小时的速度和两辆火车同时启动,从北京出发,碰到另一辆车后就向相反的方向返回去飞,就这样依次在两辆火车之间来回地飞,直到两辆火车相遇。请问,这只鸟共飞行了多长的距离?
分析:鸟在火车相遇前一直在飞,所以不论它如何往返,鸟飞的距离就是其速度乘时间,而时间则是用两列火车相遇的时间。设北京到广州的距离为 D,那么火车相遇时间是:D / (15+20),由此可得鸟飞的距离是:30 * 时间 = 30/35 * D。
解答:北京到广州距离的 30/35
4. 药丸问题
- 问题:你有四个装药丸的罐子,每个药丸都有一定的重量,被污染的药丸是没被污染的药丸的重量+1。只称量一次,如何判断哪个罐子的药被污染了?
- 解答:设未被污染的每个药丸的重量是x,则被污染的每个药丸的重量是x+1。将4个罐子分别标注为1,2、3、4,取一号罐子1个药丸,二号罐子2个药丸,三号罐子3个药丸,四号罐子4个药丸,一起称重。则:
若一号罐子药丸被污染,则重量为(10x+1);
若二号罐子药丸被污染,则重量为(10x+2);
若三号罐子药丸被污染,则重量为(10x+3);
若四号罐子药丸被污染,则重量为(10x+4)。
即称得的重量是10X+t,t是几就是第几个罐子污染了。
关键点是要区分哪个罐子被污染了,因此如果每个罐子拿出来一个药丸然后称量,虽然能得出有罐子被污染了,但是因为药丸没有编号,因此不知道污染药丸是哪个罐子的。
当然也可以取三个罐子的,如果是6+t,那么t对应前三个罐子的编号,如果t=0,说明是第四个罐子被污染了。
5. 人民币问题
- 问题:人民币为什么只有1、2、5、10的面值?
- 解答:可以用三张以内组成任何面额。
首先,1、2、5的组合可以用最少纸币数量覆盖 1-0的任意金额:
- 1是所有自然数的单位,必须存在;
- 2是最小的偶数,可与 1 组合生成 3(1+2)、4(2+2);
- 5是 10 的一半,与 1、2 组合后能高效生成 6-9(如 5+1=6,5+2=7,5+2+2=9)。
其次,10 是十进制的基数,其倍数(20、50、100)能高效覆盖更大金额,且与 1、2、5 形成体系化结构
6. 开关问题
问题:门外三个开关分别对应室内三盏灯,线路良好,在门外控制开关时候不能看到室内灯的情况,现在只允许进门一次,确定开关和灯的对应关系?
解答:设三个开关是1、2、3。打开开关1等半个小时,关上开关1并打开开关2。进房后去摸灯泡,热的是开关1对应的灯泡;亮的是开关2对应的灯泡;不亮不热的是开关3对应的灯泡。
7. 烧绳计时问题
问题: 烧一根不均匀的绳,从头烧到尾总共需要1个小时。现在有若干条材质相同的绳子,问如何用烧绳的方法来计时一个小时十五分钟呢?
解答:
- 先把1根绳子从两头点燃,燃烧完毕后刚好30分钟。
- 在第1根绳子点燃的同时,从一头点燃第2根,那么在第1根然后完毕后(30分钟),再把第2根绳子未点燃的那一头点燃,燃烧完毕后用去了45分钟(30+15)。
- 在第2根绳子燃烧完毕后,从两头点燃第3根绳子,等第3根燃烧完毕后,刚好1小时15分钟(45+30)。
8. 果冻问题
- 问题:le
- 解答:鸽巢原理
鸽巢原理的应用
- 基本原理:
若将 n 个物品放入 m 个容器,当 n>m 时,至少有一个容器中会有超过一个物品。 - 对应关系:
- 颜色种类(容器):3 种(红、绿、蓝)。
- 抓取的果冻(物品):假设抓取 k 个果冻。
- 目标:确保至少有一个颜色(容器)中有 2 个果冻(物品)。
- 数学推导:
根据鸽巢原理,当 k>3 时,至少有一个颜色会被抓取 2 次。因此,最小的 k 是 3+1=4。
把红绿蓝三个颜色当成三个容器,往里面依次同数量放果冻,当放到第几个果冻的时候,有一个容器中物品的数量会超过1个。
当放入第四个的时候,肯定有一个容器中有两个物品。
9. 量水问题
问题:如果你有无穷多的水,一个3公升的提捅,一个5公升的提捅,两只提捅形状上下都不均匀,问你如何才能准确称出4公升的水?
分析:这个题目等价于:已知两个数3和5,可用运算符+和-,要求+和-号的一端必须是3或5,并且中间结果不能大于5,列出一个结果等于4的表达式。
解答:
解法一:5 - (3 - (5 - 3))
- 用5升桶满桶,倒入3升桶中,倒满后大桶里剩2升;
- 把3升桶倒空,把那2升倒入3升桶中;
- 用5升桶满桶再向3升里倒,倒入一升就满,大桶里剩下的是4 升。
解法二:3 -(5 - 3) + 3
- 两次将3升桶满桶,倒入5升桶中,倒满后3升桶中剩1升;
- 将5升桶倒空,把3升桶中的1升倒入5升桶中;
- 将3升桶满桶倒入5升桶中。现在5升桶中包含4升。
10. 诚实国和说谎国问题
- 问题:一个岔路口分别通向诚实国和说谎国。来了两个人,已知一个是诚实国的,另一个是说谎国的。诚实国永远说实话,说谎国永远说谎话。现在你要去说谎国,但不知道应该走哪条路,需要问这两个人。请问应该怎么问?
- 分析:如果问 “哪边是诚实国?” 或者 “哪边是说谎国?” 这样的问题,由于正确答案只有固定的一边,所以两个人给出的答案必定不同。所以只能问对每个人有不同正确答案的问题,比如“你的国家在哪边?”或者“他的国家在哪边”。对应着两个问题,诚实国的人会给出诚实国方向和说谎国方向,说谎国的人也会给出诚实国和说谎国方向。这样我们就可以判断哪边是诚实国,哪边是说谎国了。
- 解答:问“你的国家怎么走? ”他们都会指向诚实国,则走另一条路即可。
11. 4人过桥问题
问题:4 个人晚上要穿过一座索桥回到他们的营地。可惜他们手上只有一支只能再坚持17分钟的手电筒。通过索桥必须要拿着手电,而且索桥每次只能撑得起两个人的份量。这四个人过索桥的速度都不一样,第一个走过索桥需要1分钟,第二个2分钟,第三个5分钟,最慢的那个要10分钟。他们怎样才能在17分钟内全部走过索桥?
分析:
过桥走法 花费时间 第一个和第二个一起过去 2 分钟 第一个回来 1分钟 第三个和第四个一起过去 10分钟 第二个回来 2 分钟 第一个和第二个一起过去 2 分钟 解答:总共花时 2 + 1 + 10 + 2 + 2 = 17 分钟。
其他策略对比
- 错误策略 1:让最慢者单独过桥
- 若先让 D(10 分钟)单独过桥,A 返回(1 分钟),再让 C(5 分钟)单独过桥,A 返回(1 分钟),最后 A 和 B 过桥(2 分钟)。
- 总时间:10+1+5+1+2=19 分钟(超时)。
- 错误策略 2:让次快者返回
12. 拿硬币问题
问题:16个硬币,A和B轮流拿走一些,每次拿走的个数只能是1,2,4中的一个数。谁最后拿硬币谁输。请问:A或B有无策略保证自己赢?
解答:B可以保证自己赢。
- 如果A拿1个,则B拿2个;
- 如果A拿2个,则B拿1个;
- 如果A拿4个,则B拿2个。
这样每次AB加起来都是3或者6,所以最后会剩下1个或4个。- 如果是1个则A直接输了;
- 如果剩下4个,A全拿则输了,如果不全拿,B继续采取上面的策略,最后还是剩下1个,还是A输。
必输点推导
当剩余硬币数为 n 时,无论当前玩家拿 1、2 还是 4 个,对手都能获胜,则 n 为必输点。
- n=1:必输点(必须拿 1 个,输)。
- n=2:拿 1 个,对手面对 n=1(必输),因此 n=2 是必胜点。
- n=3:拿 2 个,对手面对 n=1(必输),因此 n=3 是必胜点。
- n=4:
- 拿 1 个 → n=3(必胜点)。
- 拿 2 个 → n=2(必胜点)。
- 拿 4 个 → 直接拿完,输。
无论怎么拿,对手都能赢,因此 n=4 是必输点。
- n=5:拿 1 个 → n=4(必输点),因此 n=5 是必胜点。
- n=6:拿 2 个 → n=4(必输点),因此 n=6 是必胜点。
- n=7:
- 拿 1 个 → n=6(必胜点)。
- 拿 2 个 → n=5(必胜点)。
- 拿 4 个 → n=3(必胜点)。
无论怎么拿,对手都能赢,因此 n=7 是必输点。
规律总结:必输点为 n=1,4,7,10,13,16(每次递增 3)
- 因此,当A先拿1个,为了让A处于必输点,B可以拿2个,此时n=13;
- 当A先拿2个,为了让A处于必输点,B可以拿1个,此时n=13;
- 当A先拿4个,为了让A处于必输点,B可以拿2个,此时n=10;
13. 辩论赛问题
- 问题:1000个人参加辩论赛,1对1进行辩论,淘汰输掉的一方,问需要安排多少场比赛才能角出冠军?
- 解答:每场辩论赛只能淘汰一个人,要淘汰999个人则需要安排999场比赛。
14. 火车运煤问题
问题:你是山西的一个煤老板,你在矿区开采了有 3000 吨煤需要运送到市场上去卖,从你的矿区到市场有1000公里,你手里有一列烧煤的火车,这个火车最多只能装1000吨煤,且其能耗比较大,每一公里需要耗一吨煤。请问,怎么运送才能运最多的煤到集市?
解答:
1: 满运到200处卸货600回
2: 满运到200处卸货600回
3: 满运到200处卸货800停
4: 满运到533处卸货334回
5: 满运到533处卸货667停
6: 满运到终点停, 533处留一吨, 终点剩下533吨。
可以分段,将整个1000公里分为1000–500–200三个区间,首先将所有煤炭运到200处,此时还剩2000吨煤炭;然后满运到500处,此时还剩1100吨煤炭,然后一次性运到1000处,还剩500吨煤炭(还有100必须放在500节点处,已经超载)。为了节省留下的100吨煤炭,因此可以将500的节点往前提,提到533处是最优解,只需留下1吨煤炭。
15.旅馆的1元钱问题
- 问题:有三个人去住旅馆,住三间房,每一间房10元,于是他们一共付给老板30,第二天,老板觉得三间房只需要25元就够了,于是叫小弟退回5元给三位客人,谁知小弟贪心,只退回每人1元,自己偷偷拿了2元,这样以来便等于那三位客人每人各花了9元,于是三个人一共花了27元(本来花了30,结果被退回了3,相当于只花了27),再加上小弟独吞了2元,总共是29元.可是当初他们三个人一共付出30元,那么还有1元呢?
- 解答:这道题其实偷换了概念,他们所消费的27元里已经包括小弟贪污的2元了,再加退还的3元=30元。这30元的分布是:老板拿了25元,小弟拿了2元,三人各拿了1元。
- 这里加的不对,我已经将退的3元减去了,因此实际上花了27,不能是27+2,因为剩下的3是退回的而不是小弟的钱,小弟贪污的包括在27以内。
16. 老虎吃羊问题
问题:在岛上有100只老虎和1只羊,老虎可以吃草,但他们更愿意吃羊。如果每次只有一只老虎可以吃羊,而且一旦他吃了羊,他自己就变成羊;而且所有的老虎都是聪明而且完全理性的,他们的第一要务是生存。请问最后这只羊会不会被吃?如果是n只老虎和一只羊呢?
解答:
- 1只老虎,肯定吃;
- 2只老虎肯定不吃,否则就被另一只吃了;
- 3只老虎,如果一只老虎吃掉了羊,这样问题就转换为2只老虎和1只羊的情况,显然另外两种老虎不敢轻举妄动,所以羊会被吃;
- 4只老虎,如果某一只老虎吃了羊,问题转化为3只老虎和1只羊的问题,它肯定会被接下来的某一只吃掉,然后其他两只只能等着,所以4只老虎,大家都不敢吃羊;
- 归纳:我们就可以发现如果老虎数目是奇数,那么羊肯定被吃,如果是偶数,那么羊肯定不会被吃。
17. 假钱亏损问题
- 问题:王小姐是卖鞋的,一双鞋进货价45元,甩卖30元。顾客来买两双鞋给了一张100元,王小姐没有零钱,于是找了邻铺兑换了100元零钱,找给顾客40元。事后邻铺发现钱是假的,王小姐无奈又赔了邻铺100元。请问,王小姐一共亏了多少元?
- 解答:亏130 元
解法一:
- 王小姐本来甩卖每一双都会亏15元
- 这里顾客买了两双鞋,就算钱是真的,王小姐也会因甩卖亏30元
- 但如果钱是假的,那么其实王小姐一元也没挣,亏了100+30=130
解法二:
- 换钱的邻铺并没有赚钱,也没赔钱;
- 使假币的顾客相当于没花钱得到 2 双鞋(45 * 2 = 90)加上 40 元真币,所以相当于赚了 130 元;
- 所以最终是王小姐亏了 130 元。
18. 赛马问题
问题:25 匹马,每匹马的速度都不一样。因为只有 5 条跑道,所以一次竞赛只能跑 5 匹马,问最少需要多少次竞赛才能找到最快的 3 匹马?
分析:
25 = 5 * 5,首先将所有的马分为5组,每组5匹进行比赛;
假设5次竞赛后的结果是:
假设比赛结果 比赛次数 1>2>3>4>5 第1次 6>7>8>9>10 第2次 11>12>13>14>15 第3次 16>17>18>19>20 第4次 21>22>23>24>25 第5次 将 1、6、11、16、21 再比一次,假设结果是:
假设比赛结果 比赛次数 1>6>11>16>21 第6次 那么接下来最快的三匹马只可能在以下马中产生:
1 > 2 > 3;
6 > 7;
11;1是最快的马,接下来只需再比一次 2、3、6、7、11,即可知道另外两匹最快的马了;
假设比赛结果 比赛次数 11>7>6>2>3 第7次 由此可得最快的三匹马是 1、11、7。
解答:至少需要7次。
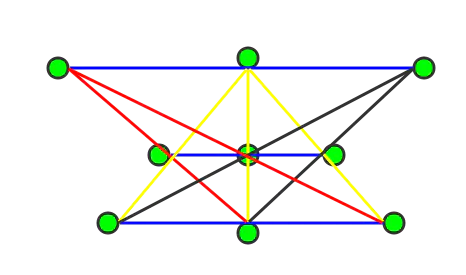
19. 九点连十线问题
问题:在9个点上画10条直线,要求每条直线上至少有三个点?
解答:
解法一:三横一竖 + 六斜 (如下图)
解法二:三竖一横 + 六斜(与解法一类似,如下图)
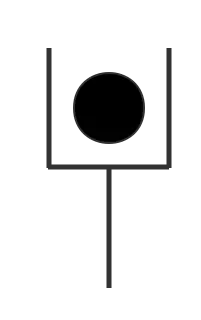
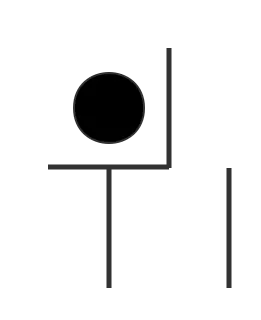
20. 移动竹签问题
问题:如下图,只能移动两根竹签,而且形状不能改变,把围住的鸡蛋给移出来。(来自《少年包青天第一部》,第13集2分40秒 包拯到杂货店里买米,店老板出的题。)
解答:
第一步:
第二步:
21. 掰巧克力问题
- 问题:一块
N*M大小的巧克力,每次掰一块的一行或一列,全部掰成1*1大小的巧克力需要掰多少次? - 解答:
N*M-1次。因为不管怎么掰,每次只能把一个大块掰成两个小块,即每次掰总块数增加1;那么将1块巧克力掰成N*M块小巧克力就需要掰N*M-1次。
22. 分蛋糕问题
问题:一个人在吃蛋糕前都会随机决定要切几刀,而且保证切完之后得到最多块蛋糕(只能垂直于底面切)。有时候切得太多他自己都忘记掉切完有几块,为了确保他能吃到整个蛋糕,他得知道切完后的蛋糕的数量。
分析:每次切割相当于在平面上画一条直线,且每一刀尽可能与之前所有直线相交,以产生最多块数。
解答:
推导过程:
第 1 刀:将蛋糕分为 2 块。
第 2 刀:与第 1 刀相交,新增 2 块,共 4 块。
第 3 刀:与前 2 刀相交,新增 3 块,共 7 块。
递推规律:第 k 刀新增 k 块,总块数为
1+1+2+3+⋯+n。
$$
1+n(n+1)/2
$$
23. 时针分针秒针重合问题
- 问题:在24小时里面时针分针秒针可以重合几次
- 解答:在 24 小时内,时针、分针、秒针完全重合的次数为 2 次,分别发生在 0 点整 和 12 点整。以下是详细分析:
- 时针与分针的重合规律:
- 时针每小时转 30°,分针每分钟转 6°(12小时中时针走1圈,而分针走12圈)
- 每 12 小时内,时针与分针重合 11 次,24 小时内重合 22 次。
- 重合时间为
t=12k/11小时(k=0,1,…,10)。
- 秒针的参与条件:
- 秒针每分钟转 360°,仅在 整点(如 0:00:00、12:00:00)时与分针、时针同时指向 12 点。
- 非整点时,秒针的角度与时针、分针无法完全一致。
- 数学验证:
- 设经过时间 t分钟,三针角度分别为:
- 时针:0.5t 度
- 分针:6t 度
- 秒针:360(t−⌊t⌋) 度(⌊t⌋ 为整数分钟部分)。
- 重合需满足:0.5t≡6t≡360(t−⌊t⌋)(mod360)
- 解得 t=720k 分钟(k=0,1),对应 0 点 和 12 点。
- 设经过时间 t分钟,三针角度分别为:
- 时针与分针的重合规律:
24. 箱子开锁问题
问题:A、B两人分别在两座岛上。B生病了,A有B所需要的药。C有一艘小船和一个可以上锁的箱子。C愿意在A和B之间运东西,但东西只能放在箱子里。只要箱子没被上锁,C都会偷走箱子里的东西,不管箱子里有什么。如果A和B各自有一把锁和只能开自己那把锁的钥匙,A应该如何把东西安全递交给B?
解答:
- A 把药放进箱子,用自己的锁把箱子锁上;
- B 拿到箱子后,再在箱子上加一把自己的锁;
- 箱子运回 A 后,A 取下自己的锁;
- 箱子再运到 B 手中时,B 取下自己的锁,获得药物。
25. 沙漏计时问题
问题:有一个能计时6分钟的小沙漏和一个能计时8分钟的大沙漏,如何计时10分钟?
解答:
- 两个沙漏同时倒置开始计时,等小沙漏漏完,大沙漏还剩2分钟,这时倒置小沙漏继续计时;
- 大沙漏漏完小沙漏还剩4分钟,再把大沙漏倒置继续计时;
- 小沙漏漏完大沙漏还剩4分钟,这时准备工作已经完毕;
- 等待大沙漏漏完(4分钟)+小沙漏(6分钟)=10分钟。
26. 人鬼过桥问题
- 问题:有三个人跟三个鬼要过河,河上没桥只有条小船,然后船每次最多载 2 个(人或鬼),无论在哪边岸上,只有是人比鬼少的情况下(如两鬼一人,三鬼两人,三鬼一人),人会被鬼吃掉,然而船有一定需要人或鬼操作才能航行(要有人或鬼划船),问,如何安全的把三人三鬼渡过河对岸?
- 解答:
| 步骤 | 操作 | 左岸状态(人,鬼) | 右岸状态(人,鬼) | 船位置 |
|---|---|---|---|---|
| 1 | 2 鬼过河 | (3, 1) | (0, 2) | 右岸 |
| 2 | 1 鬼返回 | (3, 2) | (0, 1) | 左岸 |
| 3 | 2 鬼过河 | (3, 0) | (0, 3) | 右岸 |
| 4 | 1 鬼返回 | (3, 1) | (0, 2) | 左岸 |
| 5 | 2 人过河 | (1, 1) | (2, 2) | 右岸 |
| 6 | 1人1鬼过河 | (0, 0) | (3, 3) | 右岸 |
27. 吃药片问题
问题:某种药方要求非常严格,你每天需要同时服用A、B两种药片各一颗,不能多也不能少。这种药非常贵,你不希望有任何一点的浪费。一天,你打开装药片A的药瓶,倒出一粒药片放在手心;然后打开另一个药瓶,但不小心倒出了两粒药片。现在,你手心上有一颗药片A,两颗药片B,并且你无法区别哪个是A,哪个是B。你如何才能严格遵循药方服用药片,并且不能有任何的浪费?
解答:
- 把手上的三片药各自切成两半,分成两堆摆放;
- 再取出一粒药片 A,也把它切成两半,然后在每一堆里加上半片的 A;
- 现在,每一堆药片恰好包含两个半片的 A 和两个半片的 B;
- 一天服用其中一堆即可。
28. 火枪手决斗,谁活下来的概率大?
问题:彼此痛恨的甲、乙、丙三个抢手准备决斗。甲枪法最好,十发八中;乙枪法次之,十发六中;丙枪法最差,十发四中。如果三人同时开枪,并且每人每轮只发一枪;那么枪战后,谁活下来的机会大一些?
解答:枪法最糟糕的丙活下来的几率最大,前提是三人都清楚了解对手的实力。
分析:
A. 第一轮枪战- 甲的最佳策略:先瞄准乙。因为乙对甲的威胁要比丙大,所以应该首先干掉乙。
- 乙的最佳策略:先瞄准甲。一旦将甲干掉了,和丙进行对决,乙胜算的概率要大得多。
- 丙的最佳策略:也是先瞄准甲。毕竟对丙来说,乙的威胁还是比甲要小一些,先努力干掉甲再想如何面对乙,这是丙的正常思路。
在这种情况下,我们计算一下三个枪手开枪后各自存活的概率:
- 甲存活:那就是乙丙都射偏。乙命中率60%,射偏概率是40%;丙命中率40%,射偏概率是60%。干是两人都射偏的概率40%X60%=24%,这就是甲存活的概率。
- 乙存活:那就是甲射偏。甲命中率80%,射偏概率是20%,这就是乙存活的概率。
- 丙存活:由于第一轮里无人将枪口指向丙,所以他存活概率是100%。
结论:第一轮枪战,枪法最差的丙竟然存活概率最大——肯定存活,而枪法好的甲和乙存活概率远低于丙。
B. 第二轮枪战
第一轮后,丙有可能面对甲,也可能面对乙,甚至同时面对甲与乙,或者是甲乙皆死。- 如果丙同时面对甲乙,则回到第一轮的情况。
- 如果甲乙皆死,则枪战结束,丙存活。
- 而如果丙单独面对甲或乙,命中率最低的丙的日子是最不好过的。
在这种情况下,我们再计算一下三个枪手开枪后各自存活的概率:
甲存活:
- 第一轮甲活乙死(24%*80%),第二轮甲活(60%);
- 第一轮甲乙同活(24%*20%),重复第一轮,第二轮甲活(24%)
那么甲存活概率为:(
24%*80%*60%)+(24%*20%*24%)=12.672% 乙存活:
- 第一轮乙活甲死(20%*76%),第二轮乙活(60%);
- 第一轮甲乙同活(24%*20%),重复第一轮,第二轮乙活(20%)
那么乙存活概率为:(20%*76%*60%)+(24%*20%*20%)=10.08%
丙存活:
- 第一轮甲活乙死(24%*80%),第二轮丙活(20%);
- 第一轮乙活甲死(20%*76%),第二轮丙活(40%);
- 第一轮甲乙同活(24%*20%),重复第一轮,第二轮丙活(100%);
- 第一轮甲乙同死(76%*80%),枪战结束,丙活(100%)。
那么丙存活概率为:
(24%*80%*20%)+(20%*76%*40%)+(24%*20%*100%)+(76%*80%*100%)=75.52%